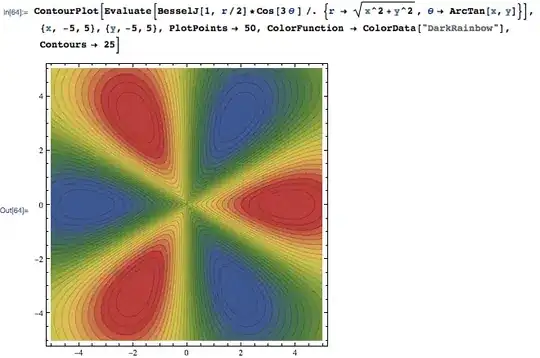
I am looking to plot something like the whispering gallery modes -- a 2D cylindrically symmetric plot in polar coordinates. Something like this:

I found the following code snippet in Trott's symbolics guidebook. Tried running it on a very small data set; it ate 4 GB of memory and hosed my kernel:
(* add points to get smooth curves *)
addPoints[lp_][points_, \[Delta]\[CurlyEpsilon]_] :=
Module[{n, l}, Join @@ (Function[pair,
If[(* additional points needed? *)
(l = Sqrt[#. #]&[Subtract @@ pair]) < \[Delta]\[CurlyEpsilon], pair,
n = Floor[l/\[Delta]\[CurlyEpsilon]] + 1;
Table[# + i/n (#2 - #1), {i, 0, n - 1}]& @@ pair]] /@
Partition[If[lp === Polygon,
Append[#, First[#]], #]&[points], 2, 1])]
(* Make the plot circular *)
With[{\[Delta]\[CurlyEpsilon] = 0.1, R = 10},
Show[{gr /. (lp : (Polygon | Line))[l_] :>
lp[{#2 Cos[#1], #2 Sin[#1]} & @@@(* add points *)
addPoints[lp][l, \[Delta]\[CurlyEpsilon]]],
Graphics[{Thickness[0.01], GrayLevel[0], Circle[{0, 0}, R]}]},
DisplayFunction -> $DisplayFunction, Frame -> False]]
Here, gr is a rectangular 2D ListContourPlot, generated using something like this (for example):
data = With[{eth = 2, er = 2, wc = 1, m = 4},
Table[Re[
BesselJ[(Sqrt[eth] m)/Sqrt[er], Sqrt[eth] r wc] Exp[
I m phi]], {r, 0, 10, .2}, {phi, 0, 2 Pi, 0.1}]];
gr = ListContourPlot[data, Contours -> 50, ContourLines -> False,
DataRange -> {{0, 2 Pi}, {0, 10}}, DisplayFunction -> Identity,
ContourStyle -> {Thickness[0.002]}, PlotRange -> All,
ColorFunctionScaling -> False]
Is there a straightforward way to do cylindrical plots like this?.. I find it hard to believe that I would have to turn to Matlab for my curvilinear coordinate needs :)