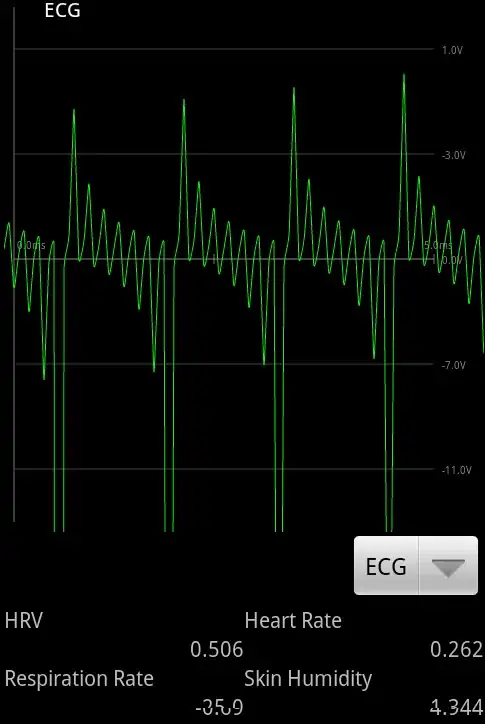
My problem is the optimization issue for SVIGP in the US Flight dataset. I implemented the SVGP model for the US flight data mentioned in the Hensman 2014 using the number of inducing point = 100, batch_size = 1000, learning rate = 1e-5 and maxiter = 500.
The result is pretty strange end ELBO does not increase and it have large variance no matter how I tune the learning rate
Initialization
M = 100
D = 8
def init():
kern = gpflow.kernels.RBF(D, 1, ARD=True)
Z = X_train[:M, :].copy()
m = gpflow.models.SVGP(X_train, Y_train.reshape([-1,1]), kern, gpflow.likelihoods.Gaussian(), Z, minibatch_size=1000)
return m
m = init()
Inference
m.feature.trainable = True
opt = gpflow.train.AdamOptimizer(learning_rate = 0.00001)
m.compile()
opt.minimize(m, step_callback=logger, maxiter = 500)
plt.plot(logf)
plt.xlabel('iteration')
plt.ylabel('ELBO')
Result:
Added Results
Once I add more iterations and use large learning rate. It is good to see that ELBO increases as iterations increase. But it is very confused that both RMSE(root mean square error) for training and testing data increase too. Do you have some suggestions? Figures and codes shown as follows:
ELBOs vs iterations
Train RMSEs vs iterations
Test RMSEs vs iterations
Using logger
def logger(x):
print(m.compute_log_likelihood())
logx.append(x)
logf.append(m.compute_log_likelihood())
logt.append(time.time() - st)
py_train = m.predict_y(X_train)[0]
py_test = m.predict_y(X_test)[0]
rmse_hist.append(np.sqrt(np.mean((Y_train - py_train)**2)))
rmse_test_hist.append(np.sqrt(np.mean((Y_test - py_test)**2)))
logger.i+=1
logger.i = 1
And the full code is shown through link.