What is wrong with this fourier transform implementation

Question

I'm trying to implement a discrete fourier transform, but it's not working. I'm probably have written a bug somewhere, but I haven't found it yet.

Based on the following formula:

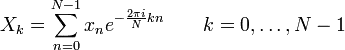
This function does the first loop, looping over X0 - Xn-1...

    public Complex[] Transform(Complex[] data, bool reverse)
    {
        var transformed = new Complex[data.Length];
        for(var i = 0; i < data.Length; i++)
        {
            //I create a method to calculate a single value
            transformed[i] = TransformSingle(i, data, reverse);
        }
        return transformed;
    }

And the actual calculating, this is probably where the bug is.

    private Complex TransformSingle(int k, Complex[] data, bool reverse)
    {
        var sign = reverse ? 1.0: -1.0;
        var transformed = Complex.Zero;
        var argument = sign*2.0*Math.PI*k/data.Length;
        for(var i = 0; i < data.Length; i++)
        {
            transformed += data[i]*Complex.FromPolarCoordinates(1, argument*i);
        }
        return transformed;
    }

Next the explaination of the rest of the code:

var sign = reverse ? 1.0: -1.0; The reversed DFT will not have -1 in the argument, while a regular DFT does have a -1 in the argument.

var argument = sign*2.0*Math.PI*k/data.Length; is the argument of the algorithm. This part:

then the last part

transformed += data[i]*Complex.FromPolarCoordinates(1, argument*i);

I think I carefully copied the algorithm, so I don't see where I made the mistake...

Additional information

As Adam Gritt has shown in his answer, there is a nice implementation of this algorithm by AForge.net. I can probably solve this problem in 30 seconds by just copying their code. However, I still don't know what I have done wrong in my implementation.

I'm really curious where my flaw is, and what I have interpreted wrong.

Answer 1

My days of doing complex mathematics are a ways behind me right now so I may be missing something myself. However, it appears to me that you are doing the following line:

transformed += data[i]*Complex.FromPolarCoordinates(1, argument*i);

when it should probably be more like:

transformed += data[i]*Math.Pow(Math.E, Complex.FromPolarCoordinates(1, argument*i));

Unless you have this wrapped up into the method FromPolarCoordinates()

UPDATE: I found the following bit of code in the AForge.NET Framework library and it shows additional Cos/Sin operations being done that are not being handled in your code. This code can be found in full context in the Sources\Math\FourierTransform.cs: DFT method.

for ( int i = 0; i < n; i++ )
{
    dst[i] = Complex.Zero;

    arg = - (int) direction * 2.0 * System.Math.PI * (double) i / (double) n;

    // sum source elements
    for ( int j = 0; j < n; j++ )
    {
        cos = System.Math.Cos( j * arg );
        sin = System.Math.Sin( j * arg );

        dst[i].Re += ( data[j].Re * cos - data[j].Im * sin );
        dst[i].Im += ( data[j].Re * sin + data[j].Im * cos );
    }
}

It is using a custom Complex class (as it was pre-4.0). Most of the math is similar to what you have implemented but the inner iteration is doing additional mathematical operations on the Real and Imaginary portions.

FURTHER UPDATE: After some implementation and testing I found that the code above and the code provided in the question produce the same results. I also found, based on the comments what the difference is between what is generated from this code and what is produced by WolframAlpha. The difference in the results is that it would appear that Wolfram is applying a normalization of 1/sqrt(N) to the results. In the Wolfram Link provided if each value is multiplied by Sqrt(2) then the values are the same as those generated by the above code (rounding errors aside). I tested this by passing 3, 4, and 5 values into Wolfram and found that my results were different by Sqrt(3), Sqrt(4) and Sqrt(5) respectfully. Based on the Discrete Fourier Transform information provided by wikipedia it does mention a normalization to make the transforms for DFT and IDFT unitary. This might be the avenue that you need to look down to either modify your code or understand what Wolfram may be doing.

Answer 2

Your code is actually almost right (you are missing an 1/N on the inverse transform). The thing is, the formula you used is typically used for computations because it's lighter, but on purely theorical environments (and in Wolfram), you would use a normalization by 1/sqrt(N) to make the transforms unitary.

i.e. your formulas would be:

Xk = 1/sqrt(N) * sum(x[n] * exp(-i*2*pi/N * k*n))

x[n] = 1/sqrt(N) * sum(Xk * exp(i*2*pi/N * k*n))

It's just a matter of convention in normalisation, only amplitudes change so your results weren't that bad (if you hadn't forgotten the 1/N in the reverse transform).

Cheers