0

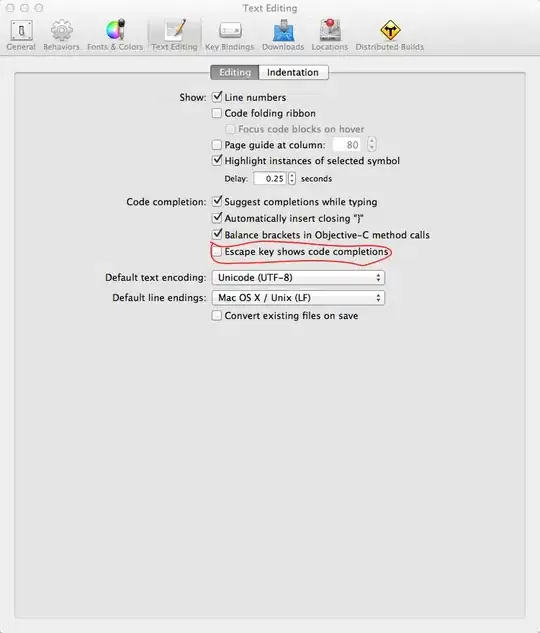
I have the following linearized plot:

enter image description here

a and b are vectors with data, c is a constant. The task is find a value of c that maximizes R^2 for a linear regression

a <- c(56.60, 37.56, 15.80, 27.65, 9.20, 5.05, 3.54)
b <- c(23.18, 13.49, 10.45, 7.24, 5.44, 4.19, 3.38)
c <- 1

x <- log(a)
y <- log((c*(a/b))-1)

rsq <- function(x, y) summary(lm(y~x))$r.squared
rsq(x, y)

optimise(rsq, maximum = TRUE)
Daniel Valencia C.
  • 2,159
  • 2
  • 19
  • 38

1 Answers1

3

This works:

a <- c(56.60, 37.56, 15.80, 27.65, 9.20, 5.05, 3.54)
b <- c(23.18, 13.49, 10.45, 7.24, 5.44, 4.19, 3.38)

rsq <- function(c) {
  x <- log(a)
  y <- log((c*(a/b))-1)
  stopifnot(all(is.finite(y)))  
  summary(lm(y ~ x))$r.squared
}
optimise(rsq, maximum = TRUE, interval=c(0.8, 3))

.

# > optimise(rsq, maximum = TRUE, interval=c(0.8, 3))
# $maximum
# [1] 1.082352
# 
# $objective
# [1] 0.8093781

You can also have a nice plot:

plot(Vectorize(rsq), .8, 3)
grid()

To set a condition for the observations you can do

rsq <- function(c) {
  xy <- data.frame(a=a, y=(c*(a/b))-1)
  summary(lm(log(y) ~ log(a), data=subset(xy, y>0)))$r.squared
}
optimise(rsq, maximum = TRUE, interval=c(0.1, 3))

... and the interesting plot:

plot(Vectorize(rsq), .3, 1.5)
grid()

rsq(0.4)
jogo
  • 12,469
  • 11
  • 37
  • 42
  • 1
    Just to be safe, you should add `stopifnot(all(is.finite(y)))` to the function. Without this condition, you can find a `c` where all y- values but one would be `NaN` and resulting r-squared would be 1. – Roland Jul 22 '19 at 12:57
  • Hi, how can I add a condition in the `function`? the rule that I want is establish a limit where `(c*(a/b)) > 1` – Daniel Valencia C. Jul 22 '19 at 17:25