Wouldn't this pseudocode give some image values greater than 255?

Question

I'm implementing the sobel filter according to the following pseudocode taken from Wikipedia:

function sobel(A : as two dimensional image array)
    Gx=[-1 0 1; -2 0 2; -1 0 1]
    Gy=[-1 -2 -1; 0 0 0; 1 2 1]

    rows = size(A,1)
    columns = size(A,2)
    mag=zeros(A)

    for i=1:rows-2
        for j=1:columns-2
            S1=sum(sum(Gx.*A(i:i+2,j:j+2)))
            S2=sum(sum(Gy.*A(i:i+2,j:j+2)))

            mag(i+1,j+1)=sqrt(S1.^2+S2.^2)
        end for
    end for

    threshold = 70 %varies for application [0 255]
    output_image = max(mag,threshold)
    output_image(output_image==round(threshold))=0;
    return output_image
end function

However, upon applying this algorithm, I'm getting many output_image values above 255, and that makes sense considering how Gx and Gy are defined. How can I modify this algorithm such that the values don't go above 255 and finally that the results look more like this?: sobel operator

--- Edit ---

There was some error in my filter implementation and I think that's why the values were above 255. After fixing the error, the values range between 0 - 16. Since now all values are below 70, applying a threshold of 70 sends everything to 0. So I set a lower threshold, 5, and multiplied the rest of the values by 10 (to enhance the edges since they are in the 5-16 range) and got the following result:

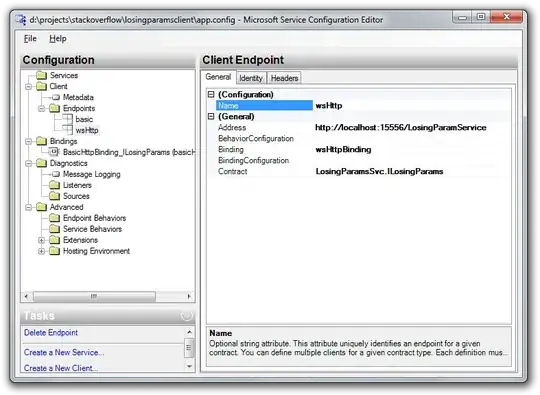
I also tried the normalization method mentioned in the comments but got a similar noisy image.

--- Edit 2 ---

Since the actual code was requested, I'm posting the code, which is written in Halide.

int main(int argc, char **argv) {
    Var x, y, k, c;
    Buffer<uint8_t> left_buffer = load_image("images/stereo/bike.jpg");
    Expr clamped_x = clamp(x, 0, left_buffer.width() - 1);
    Expr clamped_y = clamp(y, 0, left_buffer.height() - 1);
    Func left_original("left_original");
    left_original(x, y) = left_buffer(clamped_x, clamped_y);
    left_original.compute_root();

    // 3x3 sobel filter
    Buffer<uint8_t> sobel_1(3);
    sobel_1(0) = -1;
    sobel_1(1) = 0;
    sobel_1(2) = 1;

    Buffer<uint8_t> sobel_2(3);
    sobel_2(0) = 1;
    sobel_2(1) = 2;
    sobel_2(2) = 1;


    RDom conv_x(-1, 2);
    RDom conv_y(-1, 2);

    Func output_x_inter("output_x_inter");
    output_x_inter(x, y) = sum(left_original(x - conv_x, y) * sobel_1(conv_x + 1));
    output_x_inter.compute_root();
    Func output_x("output_x");
    output_x(x, y) = sum(output_x_inter(x, y - conv_y) * sobel_2(conv_y + 1));
    output_x.compute_root();

    Func output_y("output_y");
    output_y(x, y) = sum(conv_y, sum(conv_x, left_original(x - conv_x, y - conv_y) * sobel_2(conv_x + 1)) * sobel_1(conv_y + 1));
    output_y.compute_root();

    Func output("output");
    output(x, y) = sqrt(output_x(x, y) * output_x(x, y) + output_y(x, y) * output_y(x, y));
    output.compute_root();
    output.trace_stores();


    RDom img(0, left_buffer.width(), 0, left_buffer.height());

    Func max("max");
    max(k) = f32(0);
    max(0) = maximum(output(img.x, img.y));
    max.compute_root();
    Func min("min");
    min(k) = f32(0);
    min(0) = minimum(output(img.x, img.y));
    min.compute_root();

    Func output_u8("output_u8");
    // The following line sends all the values of output <= 5 to zero, and multiplies the resulting values by 10 to enhance the intensity of the edges.
    output_u8(x, y) = u8(select(output(x, y) <= 5, 0, output(x, y))*10);
    output_u8.compute_root();
    output_u8.trace_stores();



    Buffer<uint8_t> output_buff = output_u8.realize(left_buffer.width(), left_buffer.height());
    save_image(output_buff, "images/stereo/sobel/out.png");



}

--- Edit 3 ---

As one answer suggested, I changed all types to float except the last one, which must be unsigned 8-bit type. Here's the code, and the result that I'm getting.


int main(int argc, char **argv) {
    Var x, y, k, c;
    Buffer<uint8_t> left_buffer = load_image("images/stereo/bike.jpg");
    Expr clamped_x = clamp(x, 0, left_buffer.width() - 1);
    Expr clamped_y = clamp(y, 0, left_buffer.height() - 1);
    Func left_original("left_original");
    left_original(x, y) = left_buffer(clamped_x, clamped_y);
    left_original.compute_root();

    // 3x3 sobel filter
    Buffer<float_t> sobel_1(3);
    sobel_1(0) = -1;
    sobel_1(1) = 0;
    sobel_1(2) = 1;

    Buffer<float_t> sobel_2(3);
    sobel_2(0) = 1;
    sobel_2(1) = 2;
    sobel_2(2) = 1;


    RDom conv_x(-1, 2);
    RDom conv_y(-1, 2);

    Func output_x_inter("output_x_inter");
    output_x_inter(x, y) = f32(sum(left_original(x - conv_x, y) * sobel_1(conv_x + 1)));
    output_x_inter.compute_root();
    Func output_x("output_x");
    output_x(x, y) = f32(sum(output_x_inter(x, y - conv_y) * sobel_2(conv_y + 1)));
    output_x.compute_root();
    RDom img(0, left_buffer.width(), 0, left_buffer.height());

    Func output_y("output_y");
    output_y(x, y) = f32(sum(conv_y, sum(conv_x, left_original(x - conv_x, y - conv_y) * sobel_2(conv_x + 1)) * sobel_1(conv_y + 1)));
    output_y.compute_root();

    Func output("output");
    output(x, y) = sqrt(output_x(x, y) * output_x(x, y) + output_y(x, y) * output_y(x, y));
    output.compute_root();

    Func max("max");
    max(k) = f32(0);
    max(0) = maximum(output(img.x, img.y));
    max.compute_root();
    Func min("min");
    min(k) = f32(0);
    min(0) = minimum(output(img.x, img.y));
    min.compute_root();

    // output_inter for scaling 
    Func output_inter("output_inter");
    output_inter(x, y) = f32((output(x, y) - min(0)) * 255 / (max(0) - min(0)));
    output_inter.compute_root();

    Func output_u8("output_u8");
    output_u8(x, y) = u8(select(output_inter(x, y) <= 70, 0, output_inter(x, y)));
    output_u8.compute_root();
    output_u8.trace_stores();


    Buffer<uint8_t> output_buff = output_u8.realize(left_buffer.width(), left_buffer.height());
    save_image(output_buff, "images/stereo/sobel/out.png");

}

--- Edit 4 ---

As @CrisLuengo suggested, I simplified my code and outputted the result of the following:

output(x, y) = u8(min(sqrt(output_x(x, y) * output_x(x, y) + output_y(x, y) * output_y(x, y)), 255));

Since many values are way above 255, these many values are clamped to 255 and thus we get a "washed out" image:

Have you tried to normalize the mag matrix to a range of [0,255] by (mag-min)* 255/(max-min)? — Kaiwen, Jul 15 '19 at 09:31
I suggest to try a higher threshold, and check the data type of matrix A, to see whether it is double or int. Or set break points and show the intermediate result to see where the problem is — Kaiwen, Jul 15 '19 at 13:03
In general, the output of the Sobel operator as defined in the question is somewhere between -2048 and 2048. The magnitude you compute by taking the hypotenuse of the two orthogonal Sobel results is between 0 and 2048*sqrt(2). Obviously it cannot fit into a 8-bit integer, some normalization is needed. The easiest is to compute the filter using floating-point arithmetic and write the result to a floating-point image. — Cris Luengo, Jul 15 '19 at 13:13
Why don’t you show your code instead of copy-pasting pseudocode from Wikipedia? Obviously your code has a bug! — Cris Luengo, Jul 15 '19 at 13:15

score 1 · Answer 1 · answered Jul 15 '19 at 15:02

1

I don't know the Halide syntax, I've just learned it exists. But I can point out one clear problem:

Buffer<uint8_t> sobel_1(3);
sobel_1(0) = -1;

You are assigning -1 to a uint8 type. That doesn't work as intended. Make the kernel a float, and do all computations as floats, then scale the result and store it in your uint8 output image.

When computing using small integer types, one has to be very careful with overflow and underflow. The Sobel computations could likely be done in the (signed) int16 type, but in my experience there is no advantage in that over using the float type, then scaling (or clamping) and casting the result to the output image's type.

answered Jul 15 '19 at 15:02

Cris Luengo

55,762
10
62
120

Thanks for pointing that out. There's still something that I'm missing. Check out edit 3. – zengod Jul 15 '19 at 16:29
@zengod: I would simplify it a bit first by doing `output(x, y) = u8(min(sqrt(output_x(x, y) * output_x(x, y) + output_y(x, y) * output_y(x, y)), 255));`, and forgetting about `max`, `min`, and the threshold. Just look at that output, see if it is correct. – Cris Luengo Jul 15 '19 at 16:51
1

@zengod: it looks like the code is not subtracting. Maybe the float values are being cast to unsigned int within the sum? Sorry I don’t know enough about this framework to tell you how to fix this. But it is clear to me that the computations are still being done in an unsigned type. – Cris Luengo Jul 15 '19 at 18:16

score 0 · Accepted Answer · answered Jul 16 '19 at 04:30

I figured it out finally, but I'm not sure why Halide is behaving this way. When I do this:

RDom conv_x(-1, 2);
RDom conv_y(-1, 2);
Func output_x_inter("output_x_inter");
output_x_inter(x, y) = f32(sum(left_original(x - conv_x, y) * sobel_1(conv_x + 1)));
Func output_x("output_x");
output_x(x, y) = f32(sum(output_x_inter(x, y - conv_y) * sobel_2(conv_y + 1)));

Things don't work. But when I "unroll" the sum function things work:

Func output_x_inter("output_x_inter");
output_x_inter(x, y) = f32(left_original(x + 1, y) * sobel_1(0) + left_original(x, y) * sobel_1(1) + left_original(x - 1, y) * sobel_1(2));
Func output_x("output_x");
output_x(x, y) = f32(output_x_inter(x, y + 1) * sobel_2(0) + output_x_inter(x,  y) * sobel_2(1) + output_x_inter(x, y - 1) * sobel_2(2));

Wouldn't this pseudocode give some image values greater than 255?

2 Answers2