I have a np array like below:
np.array([[1,0,0],[1,0,0],[0,1,0]])
output:
array([[1, 0, 0],
[1, 0, 0],
[0, 1, 0]])
I wish to sum left diagonal and right right diagonal line elements to new array:
1) left diagonal line :
out put:
[1,1,0,1,0]
2) right diagonal line:
out put:
[0,0,1,2,0]
Is there an easy way? Thanks~
Approach #1 : Using masking
Here's a vectorized one based on masking -
def left_diag_sum_masking(a):
n = len(a)
N = 2*n-1
R = np.arange(N)
r = np.arange(n)
mask = (r[:,None] <= R) & (r[:,None]+n > R)
b = np.zeros(mask.shape,dtype=a.dtype)
b[mask] = a.ravel()
return b.sum(0)
So, left_diag_sum_masking gives us left-diagonal summations. To get the right-diagonal ones, simply flip along cols, sum and then flip it back.
Hence, simply do -
right_diag_sum = left_diag_sum_masking(a[::-1])[::-1]
Sample run -
In [220]: np.random.seed(0)
In [221]: a = np.random.randint(0,9,(4,4))
In [222]: a
Out[222]:
array([[5, 0, 3, 3],
[7, 3, 5, 2],
[4, 7, 6, 8],
[8, 1, 6, 7]])
In [223]: left_diag_sum_masking(a)
Out[223]: array([ 5, 7, 10, 23, 9, 14, 7])
In [224]: left_diag_sum_masking(a[::-1])[::-1] # right-diag sums
Out[224]: array([ 3, 5, 13, 21, 20, 5, 8])
Approach #2 : Using zeros-padding
def left_diag_sum_zerospad(a):
n = len(a)
N = 2*n-1
p = np.zeros((n,n),dtype=a.dtype)
ap = np.concatenate((a,p),axis=1)
return ap.ravel()[:n*N].reshape(n,-1).sum(0)
To get right-diagonal summations -
right_diag_sum = left_diag_sum_zerospad(a[::-1])[::-1]
Yet another method, based on padding and rolling:
def sum_shifted(arr, direction=1):
n = arr.shape[0]
temp = np.zeros((n, 2 * n - 1), dtype=arr.dtype)
temp[:, slice(None, n) if direction == 1 else slice(-n, None)] = arr
for i in range(n):
temp[i, :] = np.roll(temp[i, :], direction * i)
return np.sum(temp, 0)[::direction]
This gives you plenty of options. Speedwise, @Divakar's methods seems to have an edge:
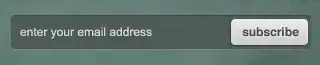
These plots were generated with this script using these as test functions:
def sum_shifted(arr, direction=1):
n = arr.shape[0]
temp = np.zeros((n, 2 * n - 1), dtype=arr.dtype)
temp[:, slice(None, n) if direction == 1 else slice(-n, None)] = arr
for i in range(n):
temp[i, :] = np.roll(temp[i, :], direction * i)
return np.sum(temp, 0)[::direction]
def sum_shifted_both(arr):
return sum_shifted(arr, 1), sum_shifted(arr, -1)
def sum_adam(arr):
return (
np.array([np.sum(np.diag(np.fliplr(arr), d)) for d in range(len(arr) - 1, -len(arr), -1)]),
np.array([np.sum(np.diag(arr, d)) for d in range(len(arr) - 1, -len(arr), -1)]))
def sum_divakar(a):
n = len(a)
N = 2*n-1
R = np.arange(N)
r = np.arange(n)
mask = (r[:,None] <= R) & (r[:,None]+n > R)
b_leftdiag = np.zeros(mask.shape,dtype=a.dtype)
b_leftdiag[mask] = a.ravel()
b_rightdiag = np.zeros(mask.shape,dtype=a.dtype)
b_rightdiag[mask[:,::-1]] = a.ravel()
return b_leftdiag.sum(0), b_rightdiag.sum(0)[::-1]
def sum_divakar2(a):
def left_sum(a):
n = len(a)
N = 2*n-1
p = np.zeros((n,n),dtype=a.dtype)
ap = np.concatenate((a,p),axis=1)
return ap.ravel()[:n*N].reshape(n,-1).sum(0)
return left_sum(a), left_sum(a[::-1])[::-1]
and as helper functions:
def gen_input(n):
return np.arange(n * n).reshape((n, n))
def equal_output(out_a, out_b):
return all(
np.all(a_arr == b_arr)
for a_arr, b_arr in zip(out_a, out_b))
input_sizes=(5, 10, 50, 100, 500, 1000, 5000)
funcs = sum_shifted_both, sum_adam, sum_divakar, sum_divakar2
runtimes, input_sizes, labels, results = benchmark(
funcs, gen_input=gen_input, equal_output=equal_output, input_sizes=input_sizes)
plot_benchmarks(runtimes, input_sizes, labels)
you can use .diag like this:
import numpy as np
arr = np.array([[1, 0, 0], [1, 0, 0], [0, 1, 0]])
left_diag = [np.sum(np.diag(np.fliplr(arr), d)) for d in range(len(arr) - 1, -len(arr), -1)]
right_diag = [np.sum(np.diag(arr, d)) for d in range(len(arr) - 1, -len(arr), -1)]
print("left:", left_diag)
print("right:", right_diag)
Output:
left: [1, 1, 0, 1, 0]
right: [0, 0, 1, 2, 0]
it returns all the element in a diagonal of a given offset. to get all the offsets in the order you mentioned, we go from +2 to -2, then for each diagonal get the sum of elements.
to get the left diagonal we first flip arr using .fliplr
A fast solution that works even for non-square matrices:
from numpy.lib.stride_tricks import as_strided
def left_diag_sum(matrix):
n_rows, n_cols = matrix.shape
if n_rows > n_cols:
matrix = matrix.T
n_rows, n_cols = n_cols, n_rows
diag_len = n_rows
n_diags = n_rows + n_cols - 1
dtype = matrix.dtype
leaning = np.zeros((diag_len, n_diags), dtype)
col_dim_stride = dtype.itemsize
row_dim_stride = col_dim_stride * (n_diags + 1)
strided = as_strided(leaning, matrix.shape, (row_dim_stride, col_dim_stride))
strided[...] = matrix
return leaning.sum(0)
def right_diag_sum(matrix):
row_reversed_matrix = matrix[::-1]
return left_diag_sum(row_reversed_matrix)[::-1]
numpy as a very useful function for this trace here is an example
''' import numpy as np a=np.array([[1,0,0],[1,0,0],[0,1,0]]) b=np.trace(a) print(b) ''' Here is the link to documentation
