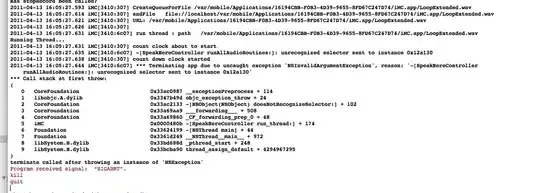
I'm trying to get an arc from a circle that is tangent to Z axis, as shown in the figure below, using matplotlib.
I just want an arc that is covered by yellow rectangle. Below is the code to get a circle.
import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
r = input('Enter the radius: ')
d = 2*r
theta = np.linspace(0, 2 * np.pi, 201)
y = d*np.cos(theta)
z = d*np.sin(theta)
for i in range(1):
phi = i*np.pi
ax.plot(y*np.sin(phi)+d*np.sin(phi),
y*np.cos(phi)+d*np.cos(phi), z)
ax.plot((0,0),(0,0), (-d,d), '-r', label='z-axis')
ax.set_xlabel('X-Axis')
ax.set_ylabel('Y-Axis')
ax.set_zlabel('Z-Axis')
ax.legend()
plt.show()
I would appreciate it if you could provide the following information,
- How can I get the arc?
- How can I change the angle of arc, that is tangent to Z-axis, on X-Y plane?

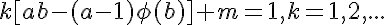

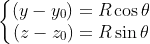
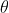 spans
spans  to have the full circle.
to have the full circle.