How can I plot a single 2-D curve onto a colormap in Matlab?

Question

I have created a smooth color gradient 2-D contour plot with existing compiled data in Matlab. I have an x-axis, y-axis, and z-data contour plotted as a colormap. My goal is to plot a 2-D curve onto the colormap, representing a single z-data value, but I don't know how.

Does anyone know how to plot a 2-D curve onto a 3-D colormap? I have provided a link to the current colormap onto which I wish to plot a single z-value as a curve.

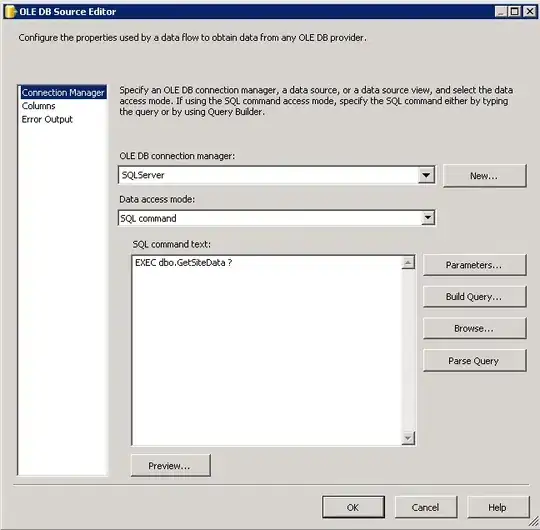
Existing colormap

x = 0.05:0.05:1;
y = 0.0:0.05:1;
[X, Y] = meshgrid(x, y);
Z = [data]
contourf(X, Y, Z);
pcolor(X, Y, Z);
shading interp
title()
xlabel()
ylabel()
colorbar

Could you [edit] your question to include the `Z = [data]` as a [Minimal, Reproducible Example](https://stackoverflow.com/help/minimal-reproducible-example) and show the output you're getting (& describe what you're wanting)? — SecretAgentMan, Jun 27 '19 at 13:44
I just added a link for you to see the colormap I already have! I'm wanting to plot a since transmissivity value (z-data) onto the colormap to show a specific solution. — Hannah-Rose Margavio, Jun 27 '19 at 20:19

SecretAgentMan · Accepted Answer · 2019-07-12T12:15:32.053

Thanks to @Cris Luengo for his comments directing me to contourc. Notice that contourc returns the isolines. According to the documentation,

To compute a single contour of level k, use contourc(Z,[k k])

which implies we can identify specific values for the isolines (values of Z) with
v = [.5 0.75 .85];
and then just use a loop to iteratively get the info needed using

for k = 1:length(v)
    Ck = contourc(x,y,Z,[v(k) v(k)]);`
end

which allows us to pass the info to plot(...) in the code below.

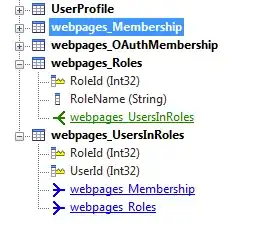
% MATLAB R2018b
x = 0:0.01:1;
y = 0:0.01:1;
[X,Y] = meshgrid(x,y);
Z = sqrt(X.^3+Y);     % Placeholder
v = [.5 0.75 .85];    % Values of Z to plot isolines

figure, hold on
pcolor(X, Y, Z); 
shading interp
colorbar
for k = 1:length(v)
    Ck = contourc(x,y,Z,[v(k) v(k)]);
    plot(Ck(1,2:end),Ck(2,2:end),'k-','LineWidth',2)
end

Old but works: Will delete once above answer finalized

Disclaimer: There may be an easier way to do this. See note at bottom.

x = 0:0.01:1;
y = 0:0.01:1;
[X,Y] = meshgrid(x,y);
Z = sqrt(X.^3+Y);          % Placeholder

The plot command can overlay anything you want on top. Or you can use contourf and specify the contours marked, including highlighting individual contours. I've illustrated two approaches—I believe the one you're looking for uses hold on; plot(...) as demonstrated below & with the left image.

In the left figure, you'll see I used logical indexing.

val = 0.75;         % Value of Z to plot contour for
tol = .002;         % numerical tolerance
idxZval = (Z <= val+tol) & (Z >= val-tol);

The success of this approach greatly depends on how fine the mesh is on Z and on the required tolerance (tol). If the Z-mesh is limited by data, then you'll have to adjust the tolerance and tune to your liking or to the limit of your data. I simply adjusted until I got the figure below and didn't tinker further.

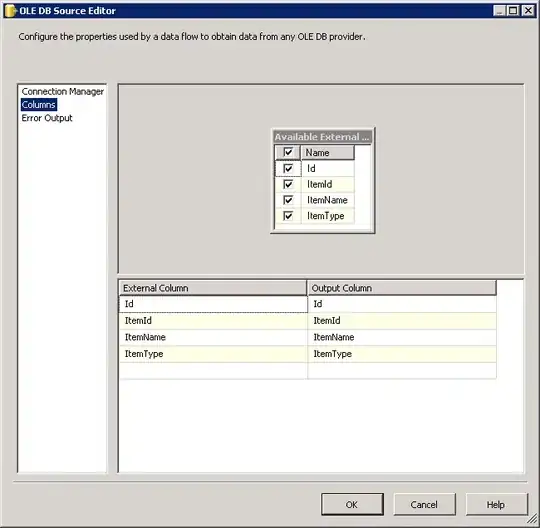
% MATLAB 2018b
figure
subplot(1,2,1) % LEFT
    pcolor(X, Y, Z); hold on
    shading interp
    xlabel('X')
    ylabel('Y')
    colorbar

    val = 0.75;         % Value of Z to plot contour for
    tol = .002;         % numerical tolerance
    idxZval = (Z <= val+tol) & (Z >= val-tol);
    plot(X(idxZval),Y(idxZval),'k-','LineWidth',2)
    title('Bootleg approach for Z = 0.75')

subplot(1,2,2) % RIGHT
    v =[0:.1:1.2]        % values of Z to plot as contours
    contourf(X,Y,Z,v)
    colorbar
    title('Contour plot specifying values v =[0:.1:1.2]')

Edit:
For future visitors, if the relationship between X,Y, and Z is known, e.g. sqrt(X.^3 + Y) = Z, then drawing a single curve for a particular Z value may be extracted from that relationship (equation) directly by solving the equation. If it is based on data instead of an analytical formula, then that may be more difficult and the approach above may be easier (thanks to @Cris Luengo for pointing this out in the comments).

Why do you say "this is an inferior approach"? I think this is the normal way: `hold on; plot(...)`. Not much to improve on that. Extracting the 2D curve could be better, e.g. by solving `sqrt(X.^3+Y)=val`, but presumably OP already has the data for the 2D curve. — Cris Luengo, Jun 27 '19 at 22:03
Just figured there was some slick way you or another MATLAB Jedi would know that I didn't. I agree that extracting the 2D curve for `plot(...)` is definitely better. Didn't go down that path since OP only include `Z = [data]` on this question what I presume is the [precursor](https://stackoverflow.com/q/55986781/8239061). — SecretAgentMan, Jun 27 '19 at 22:07
Thanks @CrisLuengo , I edited the answer and included a note at the bottom. — SecretAgentMan, Jun 27 '19 at 22:12
It looks like `contourf` uses [`contourc`](https://www.mathworks.com/help/matlab/ref/contourc.html) to compute the contour lines. `C = contourc(X,Y,Z,val)` would return the `contourMatrix` for the contour. It's a little tricky to read out, but if `val` is a single value, then `x=C(1,2:end); y=C(2,2:end);` are the coordinates to plot. (With more elements in `val` it gets tricky.) — Cris Luengo, Jun 27 '19 at 22:21
Just tried that at your suggestion. Was planning to loop through values in `val`, call `C = contourc(...)` to get the info then `plot(...)`. Requires `C = contourc(x,y,Z,val)` with `x` & `y` as vectors instead of matrices. Further, I'm unable to get `C = contourc(...)` to work unless I specify multiple values (can't do single value). — SecretAgentMan, Jun 27 '19 at 22:36
Wait. Just saw in docs, "*To compute a single contour of level `k`, use `contourc(Z,[k k])`.*" — SecretAgentMan, Jun 27 '19 at 22:39
@CrisLuengo I think you stumbled on the better approach than my goofy *tolerance*-based method. Take a look at `size(C)` for both `C = contourc(x,y,Z,[.5 .6 .7]);` and `C = contourc(x,y,Z,[.5 .5]);`. This makes me think using a loop is actually the simplest approach. — SecretAgentMan, Jun 27 '19 at 22:46
I agree! [Here](https://www.mathworks.com/help/matlab/ref/matlab.graphics.chart.primitive.contour-properties.html#budgut_-ContourMatrix) is the documentation of the output matrix of `contourc`. It's non-trivial to get the right bits of that matrix for each contour line. Just calling `contourc` in a loop is way simpler. — Cris Luengo, Jun 27 '19 at 22:55

How can I plot a single 2-D curve onto a colormap in Matlab?

1 Answers1

Linked