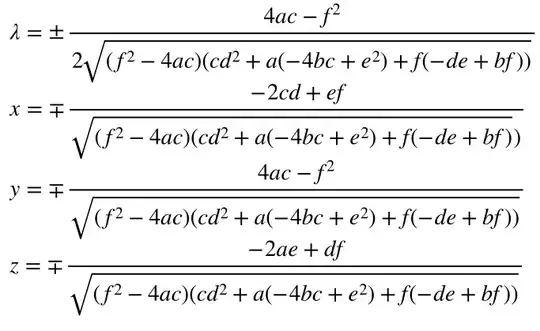3

I'm trying to write a Python code (based on a Mathematica notebook) that includes some integrations, but I had no luck so far.
The integral I'm trying to evaluate is:

Integral

where,

Ls matrices

*It's for Bjorken-Mtingwa Intra-beam scattering calculations.

In Python, what I'm trying is: 

import numpy as np
import math
from sympy import Symbol
from scipy import interpolate
import scipy.integrate as integrate
from scipy.integrate import quad

def Aint(Np, r, c , beta_rel, gamma_rel, emit_x, emit_y, Sigma_s, Sigma_M):
    return (Np * r**2 *c) / ( 64 * np.pi**2 * beta_rel**3 * gamma_rel**4 * emit_x * emit_y * Sigma_s * Sigma_M)

def MatrixSum(M1 ,M2 ,M3):
    return [[M1[i,j] + M2[i,j] + M3[i,j] for j in range (M1.shape[0])] for i in range(M1.shape[1])]

#Then I'm initializing all my parameters by loading a file into a dataframe and doing some calculations. I will not include most of that part to keep it short. I have no complex numbers.
gamma_rel = 1.00451006711
beta_rel  = 0.09465451392
beta_x = 7.890105185
beta_y = 13.61578059
Phi_x = -1.957881913
Phi_y = 0.0
emx = 2.95814809e-06
emy = 2.95814809e-06
H_x = 32.68714662287
H_y = 0.0
bl = 4.256474951
r0 = 2.16775224067e-17
Sigma_M = 0.00118124786
II = np.identity(3)

ABM = Aint(Np, r0, c, beta_rel, gamma_rel, emx, emy, bl, Sigma_M)
Clog = 13.53496204 #Evaluating the Coulomb logarithm with a function but seems correct so I will not include the calculations.

Lp = (gamma_rel**2 / Sigma_M) * np.matrix( [ [0,0,0], [0,1,0], [0,0,0] ] )
Lx = (beta_x / emx) * np.matrix( [ [1, - gamma_rel * Phi_x, 0], [- gamma_rel * Phi_x, gamma_rel**2 * H_x / beta_x , 0], [0, 0, 0] ] )
Ly = (beta_y / emy) * np.matrix( [ [0, 0, 0], [0, gamma_rel**2 * H_y / beta_y, - gamma_rel * Phi_y], [0, - gamma_rel * Phi_y, 1] ] )
L  = np.matrix(MatrixSum(Lx, Ly, Lp))

Ix = integrate.quad(lambda x: (x**(1/2.0) * (np.trace(Lx) * np.trace(np.linalg.inv(L + x * II)) - 3 * np.trace(np.matmul(Lx, np.linalg.inv(L + x * II)))) / np.linalg.det(L + x * II)**(1/2.0)) , 0, np.inf)
Ixx = 4 * np.pi * ABP * Clog * Ix[0]

#Similarly for the other 2 integrals. In reality, all 3 integrals are evaluated in a double loop.

but I am getting different results from mathematica. I have also tried scipy.integrate.simps but that did not help either.

In Mathematica, I simply integrate it with:

Ix = NIntegrate[Intx, {x, 0, inf}, MaxRecursion -> 100];

with Intx being the integral of the photo and the same procedure being done before.

Is there any recommendation for how to integrate this function efficiently? Is there something wrong with my method?

Michalis Z
  • 51
  • 6
  • Impossible to say without much more detail (i.e., the WL code). – Alan May 24 '19 at 14:49
  • I have added the code that I think is needed. I hope this helps. – Michalis Z May 27 '19 at 08:07
  • Where are you defining the identity matrix `II`? Are the results wildly different from mathematica or just slightly different? – Ali Baba May 27 '19 at 08:45
  • Just added `II`, I forgot to copy-paste it. For the calculation `Ixx = 4 * np.pi * ABP * Clog * Integral`, Mathematica gives me ~0.87 while Python ~10e-8 – Michalis Z May 27 '19 at 08:51
  • 1
    This seems to be a problem with the integral converging very slowly. Instead of integrating from `0` to `np.inf`, try integrating from `0` to `1e11` and see if you get the same result – Ali Baba May 27 '19 at 09:39
  • That helped a lot since now I have at least almost the same order of magnitude. But still, the calculation `Ixx = 4 * np.pi * ABM * Clog * Integral` gives `Ixx = 1.04941087` while Mathematica gives `Ixx = 0.8688608`. I checked ABM and Clog and I get the same values for both Mathematica and Python so, I think there is no other mistake. – Michalis Z May 27 '19 at 11:39

0 Answers0