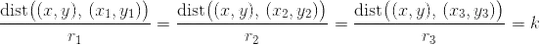Scaling 3 circles constantly until they intersect

Question

I have implemented the trilateration positioning algorithm in Python, and so far the results look quite off because of the computed distances are affected by signal interference and so it looks like this:

when it should be looking something like this:

So I was thinking about scaling the circles at the same time using a constant factor until they all intersect at one point (which would be optimal) or until the sum of their mutual distances is minimum. Given the XY coordinates of the three circles in 2D-space, as well as their FSPL-computed distances from the reference point (which is the center of one of the circles), the function should return the best scaling factor that minimizes the error. It should be something like this:

def find_best_scaling_constant(p1, p2, p3, r1, r2, r3):
  # some magic here
  return scalingConstant

find_best_scaling_constant((0.00, 0.00), (3.15, -0.47), (4.90, 7.00), 1.12, 1.77, 0.18)

I'm not a mathematician so I don't know if this logic makes sense, but if someone has a comment or a better idea, please share them. It would be of great help!

Answer 1

Let the circles have centers with coordinates:

and let the corresponding radii, you have computed, be:

respectively. So it looks like you are looking for the point and a scaling factor with the following property:

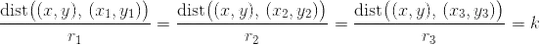
Equivalently, we need to to find a point in the plane which is the common intersection point of the three circles, obtained by re-scaling the radii of the original circles by a common factor k, or in mathematical notation, we need to solve the system

It is clear that the systems above and the property written before the system are equivalent.

To simplify things, square both sides of each equation from the system:

By Pythagoras' theorem, write

That is why, in explicit formulas, the system of three squared equations above, is in fact the quadratic system of equations:

which, after moving the term from the right-hand side of each equation to the left-hand side, becomes:

Expand all the squared differences in each equation and reorder the terms:

To simplify this system, subtract the second equation from the first, then subtract the third equation from the second and keep one of the quadratic equations, let's say keep the first quadratic equation:

The idea for finding the solution of this system, is the following:

To simplify the notation and the expressions, we can use a bit of notation from linear algebra. Define the following two by two matrix and two by one column-vectors:

and when we multiply the latter matrix equation by the inverse matrix of M:

Let us also write in matrix notation

And finally, the algorithm for finding the intersection point of the three circles, after scaling with an appropriate scaling factor, can be formulated as follows:

Observe that the quadratic equation has two solutions for z. The one I chose, with minus, is the first point of intersection whenever the three circles are external to each and with initial non-intersecting radii. There is also a second intersection point which is the one corresponding to a plus solution for z. If you have the information from a fourth tower available, then you will be able to pick the right point and possibly you may be even able to linearize the problem completely. But with this available data only, you have two solutions.

I tested the algorithm with the following hand-made example:

x1 = 0;  y1 = 0;  r1 = sqrt(13)/3;
x2 = 5;  y2 = 1;  r2 = sqrt(13)/3;
x3 = 3;  y3 = 7;  r3 = sqrt(17)/3;

and it ouputs the right location

x = 2;  y = 3;  

and scaling factor k = 3.

I implemented it in Matlab/Octave because I am comfortable with the linear algebra there:

function [xy, k] = location_scaled(x1, y1, r1, x2, y2, r2, x3, y3, r3)
        
        M = 2*[x2 - x1  y2 - y1; 
               x3 - x2  y3 - y2];
        A = [r1^2 - r2^2; 
             r2^2 - r3^2];
        B = [x2^2 + y2^2 - x1^2 - y1^2; 
             x3^2 + y3^2 - x2^2 - y2^2];
        A = M\A;
        B = M\B;
        
        a = A'*A;
        b = 2*B'*A - 2*[x1  y1]*A - r1^2;
        c = [x1 y1]*[x1; y1] - 2*[x1  y1]*B + B'*B;
        
        k = (- b - sqrt(b^2 - 4*a*c)) / (2*a);
        
        xy = k*A + B;
        k = sqrt(k);
        
end

And here is the python version:

import numpy as np

def location_scaled(x1, y1, r1, x2, y2, r2, x3, y3, r3):

        M = 2*np.array([[x2 - x1,  y2 - y1], 
                        [x3 - x2,  y3 - y2]])
        A = np.array([r1**2 - r2**2, 
                      r2**2 - r3**2])
        B = np.array([x2**2 + y2**2 - x1**2 - y1**2, 
                      x3**2 + y3**2 - x2**2 - y2**2])

        M = np.linalg.inv(M)
        A = M.dot(A)
        B = M.dot(B)
        x1_y1 = np.array([x1, y1])

        a = A.dot(A)
        b = 2*B.dot(A) - 2*x1_y1.dot(A) - r1**2
        c = x1*x1 + y1*y1 - 2*x1_y1.dot(B) + B.dot(B)

        k = (- b - np.sqrt(b*b - 4*a*c)) / (2*a);

        return k*A + B, np.sqrt(k)