5

I am doing car tracking on a video. I am trying to determine how many meters it traveled.

I randomly pulled 7 points from a video frame. I made point1 as my origin

Then on the corresponding Google Maps perspective, I calcculated the distances of the 6 points from the orgin (delta x and delta y)

Then I ran the following 

pts_src = np.array([[417, 285], [457, 794], [1383, 786], [1557, 423], [1132, 296], [759, 270], [694, 324]])

pts_dst = np.array([[0,0], [-3, -31], [30, -27], [34, 8], [17, 15], [8, 7], [6, 1]])

h, status = cv2.findHomography(pts_src, pts_dst)

a = np.array([[1032, 268]], dtype='float32')
a = np.array([a])

# finally, get the mapping
pointsOut = cv2.perspectiveTransform(a, h)

When I tested the mapping of point 7, the results are wrong.

Am I missing anything? Or am I using the wrong method? Thank you

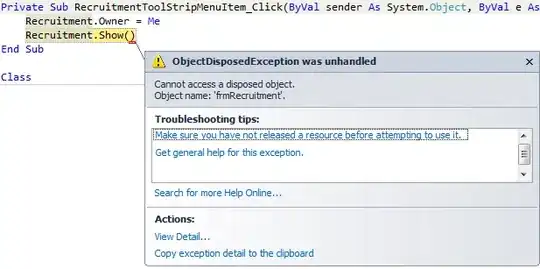
Here is the image from the video enter image description here

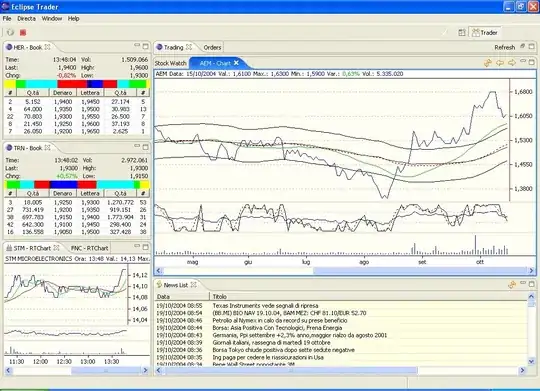
I have marked the points and here is the mapping enter image description here

The x,y column represent the pixels on the image. The metered column represent the distance from the the origin to the point in meters. I basically, usging google maps, converted the geo code to UTM and calculated the x and the y difference.

I tried to input the 7th point and I got [[[14.682752 9.927497]]] as output which is quite far in the x axis.

Any idea if I am doing anything wrong?

Snake
  • 14,228
  • 27
  • 117
  • 250

1 Answers1

5

Cameras are not ideal pinhole cameras and therefore the homography cannot capture the real transform.

For small angle cameras the result are quite close, but for a fish-eye camera the result can be very off.

Also, in my experience, just the theoretical lens distortion model found in literature is not very accurate with real-world lenses (multi-element that do "strange" things to compensate for barrel/cushion distortion). Today is also viable the use of non-spherical lenses where the transformation can be just anything.

To be able to get accurate results the only solution I found was actually mapping the transformation function using an interpolating spline function.

EDIT

In your case I'd say the problem is in the input data: considering the quasi-quadrilateral formed by the points 6, 3, 1, 2

image with marked quasi-quadrilateral

If the A-D distance in meters is 36.9, how can B-C distance be 53.8 meters?

May be the problem is in how you collected the data, or that google maps shouldn't be considered reliable for such small measurements.

A solution could be just measuring the relative distances of the points and then finding their coordinates on the plane solving from that distance matrix.

EDIT

To check I wrote a simple non-linear least squares solver (works by stochastic hill climbing) using a picture of my floor to test it. After a few seconds (it's written in Python, so speed it's not its best feature) can solve a general pinpoint planar camera equation:

 pixel_x = (world_x*m11 + world_y*m12 + m13) / w
 pixel_y = (world_x*m21 + world_y*m22 + m23) / w
 w = (x*m31 + y*m32 + m33)

 m11**2 + m12**2 + m13**2 = 1

and I can get a camera with less that 4 pixel maximum error (on a 4k image).

enter image description here

With YOUR data however I cannot get an error smaller than 120 pixels. The best matrix I found for your data is:

0.0704790534896005     -0.0066904288370295524   0.9974908226049937
0.013902632209214609   -0.03214426521221147     0.6680756144949469
6.142954035443663e-06  -7.361135651590592e-06   0.002007213927080277

Solving your data using only points 1, 2, 3 and 6 I get of course an exact numeric solution (with four general points there is one exact planar camera) but the image is clearly completely wrong (the grid should lie on the street plane):

enter image description here

6502
  • 112,025
  • 15
  • 165
  • 265
  • Thank you for the answer. Hmm I am feeling at loss with the last statement. I am not trying to go for accurate results but for as close as possible. The Camera is not fish eye camera. It is really just regular camera sitting on the corner to monitor intersection. I am trying to map points so Ican measure car speed – Snake May 13 '19 at 19:32
  • @Snake: our use requires high accuracy (~0.01%) because the camera image is used to guide a cutting machine; to get there however there is a somewhat complex calibration procedure. In your case if I understood correctly should be simpler. May be you should add a frame example to the question and the error you are getting. – 6502 May 13 '19 at 20:33
  • I added example of what I mean including how I retreived my data. Any idea? – Snake May 14 '19 at 04:13
  • Thank you for the edit. Can you elaborate more on your last line? Maybe if you explain further what you mean. Also why wouldn't 36.9 and 53.8 makes sense? The corners C and B are the furthest corners. You think they are not as far as 13 meters? – Snake May 14 '19 at 20:14
  • @Snake: I saw it and decided to check if the problem was in the data. I wrote a solver and tested with my floor tiles and I can get a pretty good precision (only pinpoint camera model, no distortion compensation). With your data however I cannot get the error below 120 pixels. I'm really convinced your input is problematic. I solved your data using only four points and overlay what is found as grid... – 6502 May 15 '19 at 21:10
  • You were absolutely right. The input seemed off. I used google earth this time. And instead of delta x and delta y in meters, I actually used Lat,Long as my destination point. I ran few tests and I got the points pretty damn close. Now I have to figure out how to convert the 2 lat,lng points into distance in meters through python (but that's a different problem). Thank you :))) – Snake May 16 '19 at 06:36