C++ Induction Algorithm very slow and Dynamical Programming

Question

I have a mathematical control problem which I solve through Backward induction. The mathematical problem is the following :

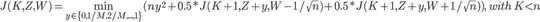RecursionFormula with K less than n. And final conditions

TerminalConditions

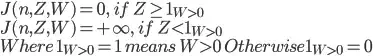
What is J(0,0,0) ?

For this purpose I am using c++ and mingw 32 bit as a compiler.

The problem is the code (below) which solve the problem is an induction and does not provide any results if n,M > 15.

I have tried to launch n=M=100 for 4 days but no results.

Does anyone have a solution? Is it a compiler option to change (the processor memory is not enough)? The complexity is too big?

Here my code

const int n = 10;
const int M = 10;

double J_naive (double K, double Z, double W)
{
    double J_tmp = exp(100.0);
    double WGreaterThanZero = 0.0;

    //Final condition : Boundaries
    if (K == n)
    {
        if (W > 0) WGreaterThanZero = 1.0;
        else WGreaterThanZero = 0.0;

        if (Z >= WGreaterThanZero) return 0.0;
        return exp(100.0);//Infinity
    }

    //Induction
    else if (K < n)
    {
        double y;
        for (int i = 0; i <= M; i++)
        {
            y = ((double) i)/M;
            {
                J_tmp = std::min (J_tmp, ((double) n)*y*y +
                                  0.5*J_naive(K+1.0, Z+y, W + 1.0/sqrt(n)) +
                                  0.5*J_naive(K+1.0, Z+y, W - 1.0/sqrt(n)) );
            }
        }
    }

    return J_tmp;
}

int main()
{
    J_naive(0.0, 0.0, 0.0);
}

`J_naive` uses recursion, and its complexity is T(n) = 2(M+1)T(n-1) (M+1 for loops, each loop calls `J_naive` twice), so T(n) ~ (2M+2)^n which is too big for M>=10 n>=10 and that's why it runs extremely slow. — tnt, May 02 '19 at 14:21
Why is `K` a `double`? It should be an `int` (doesn't really change anything but it's weird and potentially dangerous in face of changes). By the way, I don't see any dynamic programming here. Dynamic programming generally involves memorization of sub-results, which is precisely how you can potentially turn a recursion with exponential runtime into something less obnoxious (e.g. linear time for fibonacci). — Max Langhof, May 02 '19 at 14:27
It is actually very slow because it does not make use of dynamic programming to store results, and thus has an exponential complexity as mentioned above. So this is absolutely normal, as you said, 'the complexity is too big'. I'm not certain about how to use dynamic programming though, since the parameters of your recursive function are not integers. — m.raynal, May 02 '19 at 14:27
@m.raynal `K` is an integer in practice, and `W` only changes by constant deltas (of `1/sqrt(n)`) up and down, so could be represented by an integer. Similarly, Z appears to only change in (various) increments of `1/M`, so you could also represent it as an integer. — Max Langhof, May 02 '19 at 14:29
@Max yes, I should have noticed that `n` and `M` are constant, so in fact the parameters can be represented as integers and stored in a 3D-array, thanks for the remark. — m.raynal, May 02 '19 at 14:32
The usual strategy to fix an exponential-time recursion like this is dynamic programming (DP). But this is only effective if there are overlapping subproblems (that is, `J_naive()` is called multiple times with the same triple of parameter values). I think that's the case here, but there might still be too many distinct parameter triples for this to be of much benefit. A second difficulty is that DP needs to find an *exact match* for an already-solved subproblem, which is problematic for floating-point parameter values: two computations of "the same" value can easily differ in the bottom bits. — j_random_hacker, May 02 '19 at 14:33
Why does your code call `J(K+1, Z+y, ...)` when the mathematical formula says to call `J(K, Z, ...)`? Please fix the formula. Also, I have no idea what the last line in the math is supposed to say. It doesn't make sense to me. I can guess from the code, but the notation leaves the case `W < 0` completely untreated. — Max Langhof, May 02 '19 at 14:37
@MaxLanghof I have done a mistake I have just re-edited the math formula — Al Bundy, May 02 '19 at 14:48
@MaxLanghof If W < 0, since Z>=0 then Z could be equal to what you want — Al Bundy, May 02 '19 at 14:50

score 1 · Answer 1 · edited May 14 '19 at 11:59

1

You can try the following, completely untested DP code. It needs around 24*n^3*M bytes of memory; if you have that much memory, it should run within a few seconds. If there is some value that will never appear as a true return value, you can get rid of seen_[][][] and use that value in result_[][][] to indicate that the subproblem has not yet been solved; this will reduce memory requirements by about a third. It's based on your code before you made edits to fix bugs.

const int n = 10;
const int M = 10;

bool seen_[n][n * M][2 * n];       // Initially all false
double result_[n][n * M][2 * n];

double J_naive(unsigned K, unsigned ZM, double W0, int Wdsqrtn)
{
    double J_tmp = exp(100.0);
    double WGreaterThanZero = 0.0;

    double Z = (double) ZM / M;
    double W = W0 + Wdsqrtn * 1./sqrt(n);

    //Final condition : Boundaries
    if (K == n)
    {
        if (W > 0) WGreaterThanZero = 1.0;
        else WGreaterThanZero = 0.0;

        if (Z >= WGreaterThanZero) return 0.0;
        return exp(100.0);//Infinity
    }

    //Induction
    else if (K < n)
    {
        if (!seen_[K][ZM][Wdsqrtn + n]) {
            // Haven't seen this subproblem yet: compute the answer
            for (int i = 0; i <= M; i++)
            {
                J_tmp = std::min (J_tmp, ((double) n)*i/M*i/M +
                                  0.5*J_naive(K+1, ZM+i, W0, Wdsqrtn+1) +
                                  0.5*J_naive(K+1, ZM+i, W0, Wdsqrtn-1) );
            }

            result_[K][ZM][Wdsqrtn + n] = J_tmp;
            seen_[K][ZM][Wdsqrtn + n] = true;
        }
    }

    return result_[K][ZM][Wdsqrtn + n];
}

edited May 14 '19 at 11:59

Al Bundy

184
1
12

answered May 02 '19 at 15:16

j_random_hacker

50,331
10
105
169

Seems to be mistaken with n=M=100 I obtain J_SE(0,0,0) = 1.23708597424579e+043 whereas I have to get something roughly around 0.9. The positive points is your code provides a results. – Al Bundy May 02 '19 at 15:33
Is `seen_` a global variable? If not, you need to explicitly set all of its entries to `false` initially. – j_random_hacker May 02 '19 at 15:37
If that doesn't solve the problem, to debug this yourself, compare the results of my implementation with your (original) implementation, first trying the smallest values of M and n (e.g. M=1, n=1), and increasing them until you hit the first difference. – j_random_hacker May 02 '19 at 15:39
I've fixed one bug in calculating Z from ZM, please try again – j_random_hacker May 02 '19 at 15:41
Thx your code works now. Eventually, I need to know the values of J(0,0, W0 = 0) and J(0,0, W0 = 0.001) (where W0 is the value of W at time zero/at beginning) in order to compute a derivative of J around zero wrt W0. The problem is that I obtain the same values for W0 = 0.001 W0 = 0.01 W0 = 0.1 (i.e. n=M=50, J(0,0,0)= 0.873748, J(0,0,0.001)=J(0,0,0.1)= J(0,0,0.2)= 0.9192462). Which is a problem if I want to compute a derivative and J is not constant and have to be continuous with respect to W0. Do you think it is because of my 32 bits compiler ? or a problem of a double ? – Al Bundy May 14 '19 at 06:33
I think that I have to compute the code for n=M=1000 in order to see the difference but it takes too much time. Is there a way in this case to improve the speed ? – Al Bundy May 14 '19 at 06:44

C++ Induction Algorithm very slow and Dynamical Programming

1 Answers1