1

I have got two equations, one linear say,

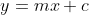formula , where m and c are constants and the other quadratic say,

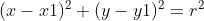another , where x1, y1 and r are constants.

Is there a way I can solve for x and y using Python ?

I could solve them on pen and paper finding the relation between x and y from the linear equation and substituting it in the other. There would be two roots satisfying the quadratic equation.

Anuradha
  • 1,089
  • 4
  • 18
  • 29

2 Answers2

1

Look at SymPy.

Here is an example of how to solve a simple difference of squares equation, taken from their documentation.

>>> from sympy.solvers import solve
>>> from sympy import Symbol

>>> x = Symbol('x')
>>> solve(x**2 - 1, x)

[-1, 1]

Regarding your specific problem, the solution will look something like this:

>>> x = Symbol('x')
>>> y = Symbol('y')

>>> solve( (x-c1)**2 + (y-c2)**2 - c3**2, x, y)

c1, c2 and c3 are the constants declared as variables earlier in your code.

Michael Oosthuizen
  • 134
  • 4
  • Yes,it does work. For particular case, I get [152 - 15*sqrt(2)/2, 15*sqrt(2)/2 + 152] as the solution. Is there a way, I can get numeric value for it? How can I solve the expression sqrt(x) ? – Anuradha Apr 29 '19 at 10:36
  • 1
    You can evaluate one root, for example `152 - 15*sqrt(2)/2`, directly. You just need to make sure `sqrt` is imported by using `from math import sqrt`. – Michael Oosthuizen May 04 '19 at 14:15
  • 1
    ```>>> from math import sqrt >>> 152 - 15*sqrt(2)/2 >>> 141.3933982822018``` – Michael Oosthuizen May 04 '19 at 14:15
0

Provided we know the constants: m, c, x1, y1, r ; the code should look like this:

import sympy as sym
x,y = sym.symbols('x,y')
Eq1 = sym.Eq(y-mx,c)
Eq2 = sym.Eq((x-x1)**2 + (y-y1)**2, r**2)
sol = sym.solve([Eq1,Eq2],(x,y))
Subhrasankha Dey
  • 36
  • 3