matlab, how do i write a statement that will give me time on xaxis from y=0.3

Question

x=[0:.01:10];
y=(x.^2).*(exp(-x));

plot(x,y), grid
y1=max(y);

xlabel('TIME');
ylabel('CONCENTRATION IN BLOOD');
title('CONCENTRATIN OF SUSTANCE IN BLOOD vs TIME');

fprintf('(a) The maximum concentraion is %f \n',y1)

That's my program, and I'm having trouble to write a statement that will give me the time at when y=0.3 please assist
thank you

Answer 1

One key issue here is that there are multiple points on your plot where y = 0.3. If you want to find all of them in a simple way, you can follow these steps:

• Subtract 0.3 from your vector y, so that the points you want to find become zero crossings.
• Find the indices in the above vector where there is a sign change.
• For the y values on either side of the zero crossings, compute the percentage of the difference between them at which the value 0.3 lies. This essentially performs a linear interpolation between the two points on either side of the zero crossing.
• Use the above percentage to find the corresponding value of x for the zero crossing.

And here's the code along with a plot to show the points found:

>> yDesired = 0.3;
>> index = find(diff(sign(y-yDesired)));
>> pctOfDiff = (yDesired-y(index))./(y(index+1)-y(index));
>> xDesired = x(index)+pctOfDiff.*(x(index+1)-x(index))

xDesired =

    0.8291    3.9528

>> plot(x,y);
>> hold on;
>> plot(xDesired,yDesired,'r*')
>> xlabel('x');
>> ylabel('y');

Answer 2

A straightforward answer is:

find(min(abs(y- 0.3))== abs(y- 0.3))

giving

ans = 84

thus

x(84)
ans = 0.83000

Now, if you increase the resolution in x, you'll also be able to find a solution closer to the analytical one.

> x=[0.5:.000001:1]; y=(x.^2).*(exp(-x));
> x(find(min(abs(y- 0.3))== abs(y- 0.3)))
ans =  0.82907

Edit:
And of'course in order to find all zeros:

> x=[0:.01:10]; y=(x.^2).*(exp(-x));
2> find(abs(y- 0.3)< 1e-3)
ans =
    84   396
> x(find(abs(y- 0.3)< 1e-3))
ans =
   0.83000   3.95000

Answer 3

If you have the symbolic toolbox in MATLAB, you can do the following

syms x
x=solve('x^2*exp(-x)=y')

x=
  (-2)*lambertw(k, -((-1)^l*y^(1/2))/2)

Here lambertw is the solution to y=x*exp(x), which is available as a function in MATLAB. So you can now define a function as,

t=@(y,k,l)(-2)*lambertw(k, -((-1)^l*y^(1/2))/2)

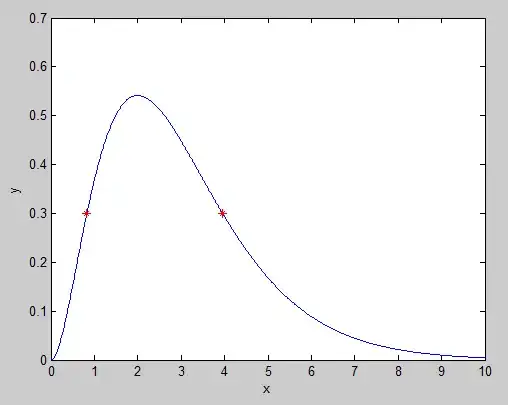
lambertw is a multivalued function with several branches. The variable k lets you choose a branch of the solution. You need the principal branch, hence k=0. l (lower case L) is just to pick the appropriate square root of y. We need the positive square root, hence l=0. Therefore, you can get the value of t or the time for any value of y by using the function.

So using your example, t(0.3,0,0) gives 0.8291.

EDIT

I forgot that there are two branches of the solution that give you real outputs (gnovice's answer reminded me of that). So, for both solutions, use

t(0.3,[0,-1],0)

which gives 0.8921 and 3.9528.

Answer 4

An easier way to find the index (and therefore x-value) is:

[minDiff, index] = min(abs(y-0.3))

minDiff =

  3.9435e-004


index =

    84

 x(index)

ans =

    0.8300

Answer 5

In addition to the solutions already posted, I am adding other ways to solve the problem:

f = @(x) (x.^2).*(exp(-x));             %# function handle
y0 = 0.3;

format long

%# find root of function near s0
x1 = fzero(@(x)f(x)-y0, 1)              %# find solution near x=1
x2 = fzero(@(x)f(x)-y0, 3)              %# find solution near x=3

%# find minimum of function in range [s1,s2]
x1 = fminbnd(@(x)abs(f(x)-y0), 0, 2)    %# find solution in the range x∈[0,2]
x2 = fminbnd(@(x)abs(f(x)-y0), 2, 4)    %# find solution in the range x∈[2,4]