Finding subarray with target bitwise AND value

Question

Given an array A of size N and an integer P, find the subarray B = A[i...j] such that i <= j, compute the bitwise value of subarray elements say K = B[i] & B[i + 1] & ... & B[j].
Output the minimum value of |K-P| among all possible values of K.

Answer 1

Here is a a quasilinear approach, assuming the elements of the array have a constant number of bits.

The rows of the matrix K[i,j] = A[i] & A[i + 1] & ... & A[j] are monotonically decreasing (ignore the lower triangle of the matrix). That means the absolute value of the difference between K[i,:] and the search parameter P is unimodal and a minimum (not necessarily the minimum as the same minimum may occur several times, but then they will do so in a row) can be found in O(log n) time with ternary search (assuming access to elements of K can be arranged in constant time). Repeat this for every row and output the position of the lowest minimum, bringing it up to O(n log n).

Performing the row-minimum search in a time less than the size of row requires implicit access to the elements of the matrix K, which could be accomplished by creating b prefix-sum arrays, one for each bit of the elements of A. A range-AND can then be found by calculating all b single-bit range-sums and comparing them with the length of the range, each comparison giving a single bit of the range-AND. This takes O(nb) preprocessing and gives O(b) (so constant, by the assumption I made at the beginning) access to arbitrary elements of K.

I had hoped that the matrix of absolute differences would be a Monge matrix allowing the SMAWK algorithm to be used, but that does not seem to be the case and I could not find a way to push to towards that property.

Answer 2

Are you familiar with the Find subarray with given sum problem? The solution I'm proposing uses the same method as in the efficient solution in the link. It is highly recommended to read it before continuing.

First let's notice that the longer a subarray its K will be it will be smaller, since the & operator between two numbers can create only a smaller number.

So if I have a subarray from i to j and I want want to make its K smaller I'll add more elements (now the subarray is from i to j + 1), if I want to make K larger I'll remove elements (i + 1 to j).

If we review the solution to Find subarray with given sum we see that we can easily transform it to our problem - the given sum is K and summing is like using the & operator, but more elements is smaller K so we can flip the comparison of the sums.

This problem tells you if the solution exist but if you simply maintain the minimal difference you found so far you can solve your problem as well.

Edit

This solution is true if all the numbers are positive, as mentioned in the comments, if not all the numbers are positive the solution is slightly different.

Notice that if not all of the numbers are negative, the K will be positive, so in order to find a negative P we can consider only the negatives in the algorithm, than use the algorithm as shown above.

Answer 3

Here an other quasi-linear algorithm, mixing the yonlif Find subarray with given sum problem solution with Harold idea to compute K[i,j]; therefore I don't use pre-processing which if memory-hungry. I use a counter to keep trace of bits and compute at most 2N values of K, each costing at most O(log N). since log N is generally smaller than the word size (B), it's faster than a linear O(NB) algorithm.

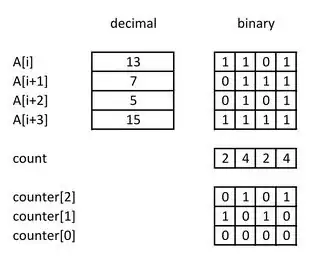
Counts of bits of N numbers can be done with only ~log N words :

So you can compute A[i]&A[i+1]& ... &A[I+N-1] with only log N operations.

Here the way to manage the counter: if

• counter is C0,C1, ...Cp, and
• Ck is Ck0,Ck1, ...Ckm,

Then Cpq ... C1q,C0q is the binary representation of the number of bits equal to 1 among the q-th bit of {A[i],A[i+1], ... ,A[j-1]}.

The bit-level implementation (in python); all bits are managed in parallel.

def add(counter,x):
    k = 0
    while x :
        x, counter[k] = x & counter[k], x ^ counter[k]
        k += 1

def sub(counter,x):
    k = 0
    while x :
        x, counter[k] = x & ~counter[k], x ^ counter[k]
        k += 1

def val(counter,count):  # return A[i] & .... & A[j-1] if count = j-i.  
    k = 0
    res = -1
    while count:
       if count %2 > 0 : res &= counter[k]
       else: res &= ~counter[k]
       count //= 2
       k += 1
    return res

And the algorithm :

def solve(A,P):
    counter = np.zeros(32, np.int64) # up to 4Go
    n = A.size
    i = j = 0
    K=P # trig fill buffer
    mini = np.int64(2**63-1)

    while i<n :

        if  K<P or j == n :     # dump buffer 
            sub(counter,A[i])
            i += 1
        else:                   # fill buffer
            add(counter,A[j])
            j += 1

        if j>i: 
            K = val(counter, count)
            X = np.abs(K - P)
            if mini > X: mini = X
        else : K = P            # reset K     

    return mini

val,sub and add are O(ln N) so the whole process is O(N ln N)

Test :

n = 10**5
A = np.random.randint(0, 10**8, n, dtype=np.int64)
P = np.random.randint(0, 10**8, dtype=np.int64)

%time solve(A,P)
Wall time: 0.8 s
Out: 452613036735

A numba compiled version (decorate the 4 functions by @numba.jit) is 200x faster (5 ms).

Answer 4

Yonlif answer is wrong.

In the Find subaray with given sum solution we have a loop where we do substruction.

while (curr_sum > sum && start < i-1)
    curr_sum = curr_sum - arr[start++];        

Since there is no inverse operator of a logical AND, we cannot rewrite this line and we cannot use this solution directly.

One would say that we can recalculate the sum every time when we increase the lower bound of a sliding window (which would lead us to O(n^2) time complexity), but this solution would not work (I'll provide the code and counter example in the end).

Here is brute force solution that works in O(n^3)

unsigned int getSum(const vector<int>& vec, int from, int to) {
    unsigned int sum = -1;
    for (auto k = from; k <= to; k++)
        sum &= (unsigned int)vec[k];
    return sum;
}

void updateMin(unsigned int& minDiff, int sum, int target) {
    minDiff = std::min(minDiff, (unsigned int)std::abs((int)sum - target));
}

// Brute force solution: O(n^3)
int maxSubArray(const std::vector<int>& vec, int target) {
    auto minDiff = UINT_MAX;
    for (auto i = 0; i < vec.size(); i++) 
        for (auto j = i; j < vec.size(); j++)                           
            updateMin(minDiff, getSum(vec, i, j), target);          
    return minDiff;
}

Here is O(n^2) solution in C++ (thanks to B.M answer) The idea is to update current sum instead calling getSum for every two indices. You should also look at B.M answer as it contains conditions for early braak. Here is C++ version:

int maxSubArray(const std::vector<int>& vec, int target) {
    auto minDiff = UINT_MAX;
    for (auto i = 0; i < vec.size(); i++) {
        unsigned int sum = -1;
        for (auto j = i; j < vec.size(); j++) {
            sum &= (unsigned int)vec[j];
            updateMin(minDiff, sum, target);
        }
    }               
    return minDiff;
}

Here is NOT working solution with a sliding window: This is the idea from Yonlif answer with the precomputation of the sum in O(n^2)

int maxSubArray(const std::vector<int>& vec, int target) {
    auto minDiff = UINT_MAX;
    unsigned int sum = -1;
    auto left = 0, right = 0;

    while (right < vec.size()) {
        if (sum > target)
            sum &= (unsigned int)vec[right++];
        else                                
            sum = getSum(vec, ++left, right);       
        updateMin(minDiff, sum, target);            
    }
    right--;
    while (left < vec.size()) {
        sum = getSum(vec, left++, right);
        updateMin(minDiff, sum, target);            
    }   
    return minDiff;
}

The problem with this solution is that we skip some sequences which can actually be the best ones.

Input: vector = [26,77,21,6], target = 5.

Ouput should be zero as 77&21=5, but sliding window approach is not capable of finding that one as it will first consider window [0..3] and than increase lower bound, without possibility to consider window [1..2].

If someone have a linear or log-linear solution which works it would be nice to post.

Answer 5

Here is a solution that i wrote and that takes time complexity of the order O(n^2). The below code snippet is written in Java .

class Solution{
    public int solve(int[] arr,int p){
        int maxk = Integer.MIN_VALUE;
        int mink = Integer.MAX_VALUE;
        int size = arr.length;

        for(int i =0;i<size;i++){
            int temp = arr[i];
            for(int j = i;j<size;j++){
                temp &=arr[j];
                if(temp<=p){
                    if(temp>maxk)
                        maxk = temp;
                }
                else{
                    if(temp < mink)
                        mink = temp;
                }
            }
        }
        int min1 = Math.abs(mink -p);
        int min2 = Math.abs(maxk -p);
        return ( min1 < min2 ) ? min1 : min2;
    }
}

It is simple brute force approach where 2 numbers let us say x and y , such that x <= k and y >=k are found where x and y are some different K = arr[i]&arr[i+1]&...arr[j] where i<=j for different i and j for x,y . Answer will be just the minimum of |x-p| and |y-p| .

Answer 6

This is a Python implementation of the O(n) solution based on the broad idea from Yonlif's answer. There were doubts about whether this solution could work since no implementation was provided, so here's an explicit writeup.

Some caveats:

1. The code technically runs in O(n*B), where n is the number of integers and B is the number of unique bit positions set in any of the integers. With constant-width integers that's linear, but otherwise it's not generally linear in actual input size. You can get a true linear solution for exponentially large inputs with more bookkeeping.
2. Negative numbers in the array aren't handled, since their bit representation isn't specified in the question. See the comments on Yonlif's answer for hints on how to handle fixed-width two's complement signed integers.

The contentious part of the sliding window solution seems to be how to 'undo' bitwise &. The trick is to store the counts of set-bits in each bit-position of elements in your sliding window, not just the bitwise &. This means adding or removing an element from the window turns into adding or removing 1 from the bit-counters for each set-bit in the element.

On top of testing this code for correctness, it isn't too hard to prove that a sliding window approach can solve this problem. The bitwise & function on subarrays is weakly-monotonic with respect to subarray inclusion. Therefore the basic approach of increasing the right pointer when the &-value is too large, and increasing the left pointer when the &-value is too small, will cause our sliding window to equal an optimal sliding window at some point.

Here's a small example run on Dejan's testcase from another answer:

A = [26, 77, 21, 6], Target = 5

Active sliding window surrounded by []


[26], 77, 21, 6
left = 0, right = 0, AND = 26

----------------------------------------
[26, 77], 21, 6
left = 0, right = 1, AND = 8


----------------------------------------
[26, 77, 21], 6
left = 0, right = 2, AND = 0


----------------------------------------
26, [77, 21], 6
left = 1, right = 2, AND = 5


----------------------------------------
26, 77, [21], 6
left = 2, right = 2, AND = 21


----------------------------------------
26, 77, [21, 6]
left = 2, right = 3, AND = 4


----------------------------------------
26, 77, 21, [6]
left = 3, right = 3, AND = 6

So the code will correctly output 0, as the value of 5 was found for [77, 21]

Python code:

def find_bitwise_and(nums: List[int], target: int) -> int:
    """Find smallest difference between a subarray-& and target.
    Given a list on nonnegative integers, and nonnegative target
    returns the minimum value of abs(target - BITWISE_AND(B))
    over all nonempty subarrays B

    Runs in linear time on fixed-width integers.
    """

    def get_set_bits(x: int) -> List[int]:
        """Return indices of set bits in x"""
        return [i for i, x in enumerate(reversed(bin(x)[2:]))
                if x == '1']

    def counts_to_bitwise_and(window_length: int,
                              bit_counts: Dict[int, int]) -> int:
        """Given bit counts for a window of an array, return 
        bitwise AND of the window's elements."""

        return sum((1 << key) for key, count in bit_counts.items()
                   if count == window_length)

    current_AND_value = nums[0]
    best_diff = abs(current_AND_value - target)

    window_bit_counts = Counter(get_set_bits(nums[0]))

    left_idx = right_idx = 0
    while right_idx < len(nums):
        
        # Expand the window to decrease & value
        if current_AND_value > target or left_idx > right_idx:
            right_idx += 1
            if right_idx >= len(nums):
                break
            window_bit_counts += Counter(get_set_bits(nums[right_idx]))
            
        # Shrink the window to increase & value
        else:
            window_bit_counts -= Counter(get_set_bits(nums[left_idx]))
            left_idx += 1

        current_AND_value = counts_to_bitwise_and(right_idx - left_idx + 1,
                                                  window_bit_counts)

        # No nonempty arrays allowed
        if left_idx <= right_idx:
            best_diff = min(best_diff, abs(current_AND_value - target))

    return best_diff