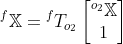How to calculate relative pose between two objects and put them in a transformation matrix

Question

I have poses of two objects. They are in terms of x,y,z and roll, pitch and yaw (I get them in quaternion and then convert them to roll,pitch,yaw). What I need to do is I will record the relative pose between two objects, record them, so, when one of the object rotates, the other is translated and rotated exactly the same way. I am getting the pose from the centroid of the objects.

This video will illustrate what I intend to do.

https://drive.google.com/file/d/1NKtS9fv-FasloVwCKqYIAV1Uc2i9_PN0/view

I have visited the following site for help:

http://planning.cs.uiuc.edu/node102.html

Please help me, I am stuck for a long time, I need a direction, I am new in robotics and I do not have any background in computer vision.

@Vik, so I have implemented as the way you wanted but it is not working properly. I am working in ROS environment in python but I have given the logic part of the code. If you could take a look, then it would be very helpful. I got my matrices from here: http://planning.cs.uiuc.edu/node104.html

#This is object2
p = PoseStamped()
p.header.frame_id = robot.get_planning_frame()
p.pose.position.x = 0.90
p.pose.position.y = 0.30
p.pose.position.z = 1.2
p.pose.orientation.x=0.0
p.pose.orientation.y=0.0
p.pose.orientation.z=0.0
p.pose.orientation.w=1.0
scene.add_box("object2", p, (0.1, 0.1, 0.2))

rospy.sleep(2)

quaternion1 =   (p.pose.orientation.x,p.pose.orientation.y,p.pose.orientation.z,p.pose.orientation.w)
euler = tf.transformations.euler_from_quaternion(quaternion1, axes='sxyz') # will provide result in x, y,z sequence
roll=euler[0]
pitch=euler[1]
yaw=euler[2]

C00=math.cos(yaw)*math.cos(pitch)
C01=math.cos(yaw)*math.sin(pitch)*math.sin(roll) - math.sin(yaw)*math.sin(roll)
C02=math.cos(yaw)*math.sin(pitch)*math.cos(roll) + math.sin(yaw)*math.sin(roll)
C03=p.pose.position.x
C10=math.sin(yaw)*math.cos(pitch)
C11=math.sin(yaw)*math.sin(pitch)*math.sin(roll) + math.cos(yaw)*math.cos(roll)
C12=math.sin(yaw)*math.sin(pitch)*math.cos(roll) -math.cos(yaw)*math.sin(roll)
C13=p.pose.position.y
C20= -math.sin(pitch)
C21=math.cos(pitch)*math.sin(roll)
C22=math.cos(pitch)*math.cos(roll)
C23=p.pose.position.z
C30=0
C31=0
C32=0
C33=1

obj2_mat=np.array([[C00, C01, C02, C03],[C10, C11, C12, C13],[C20, C21, C22, C23],[C30, C31, C32, C33]])

#This is object1
p1 = PoseStamped()
p1.header.frame_id = robot.get_planning_frame()
p1.pose.position.x = 0.9
p1.pose.position.y = 0.30
p1.pose.position.z = 0.7
p1.pose.orientation.x=0.0
p1.pose.orientation.y=0.0
p1.pose.orientation.z=0.0
p1.pose.orientation.w=1.0


scene.add_box("object1", p1, (0.1, 0.1, 0.5))


rospy.sleep(2)

quaternion2 = (p1.pose.orientation.x,p1.pose.orientation.y,p1.pose.orientation.z,p1.pose.orientation.w)
euler = tf.transformations.euler_from_quaternion(quaternion2, axes='sxyz')
roll=euler[0]
pitch=euler[1]
yaw=euler[2]

C00=math.cos(yaw)*math.cos(pitch)
C01=math.cos(yaw)*math.sin(pitch)*math.sin(roll) - math.sin(yaw)*math.sin(roll)
C02=math.cos(yaw)*math.sin(pitch)*math.cos(roll) + math.sin(yaw)*math.sin(roll)
C03=p1.pose.position.x
C10=math.sin(yaw)*math.cos(pitch)
C11=math.sin(yaw)*math.sin(pitch)*math.sin(roll) + math.cos(yaw)*math.cos(roll)
C12=math.sin(yaw)*math.sin(pitch)*math.cos(roll) -math.cos(yaw)*math.sin(roll)
C13=p1.pose.position.y
C20= -math.sin(pitch)
C21=math.cos(pitch)*math.sin(roll)
C22=math.cos(pitch)*math.cos(roll)
C23=p1.pose.position.z
C30=0
C31=0
C32=0
C33=1

obj1_mat=np.array([[C00, C01, C02, C03],[C10, C11, C12, C13],[C20, C21, C22, C23],[C30, C31, C32, C33]])

transformation_mat=np.dot(inv(obj2_mat), obj1_mat) #generating the transformation

rospy.sleep(10)

#This is object1 in second pose
p2 = PoseStamped()
p2.header.frame_id = robot.get_planning_frame()
p2.pose.position.x = 0.70
p2.pose.position.y = -0.9
p2.pose.position.z = 0.7
p2.pose.orientation.x=0.3826834
p2.pose.orientation.y=0.0
p2.pose.orientation.z=0.0
p2.pose.orientation.w=-0.9238795
scene.add_box("object1", p2, (0.1, 0.1, 0.5))

object_position_mat=np.array([[p2.pose.position.x],[p2.pose.position.y],[p2.pose.position.z],[1]]) # (x,y,z,1) position matrix for object1 in its second position

rospy.sleep(2)

Final_position=np.dot(transformation_mat, object_position_mat) #Getting the new position of object2 by multiplying transformation matrix with position of object1


print "============ Generating plan 2"


#This is object2 in second pose
p = PoseStamped()
p.header.frame_id = robot.get_planning_frame()
p.pose.position.x = Final_position[0]
p.pose.position.y = Final_position[1]
p.pose.position.z = Final_position[2]
p.pose.orientation.x=p2.pose.orientation.x #Kept the same orientation values of object1 in second pose, did not do any calculation as it is logical
p.pose.orientation.y=p2.pose.orientation.y
p.pose.orientation.z=p2.pose.orientation.z
p.pose.orientation.w=p2.pose.orientation.w

scene.add_box("object2", p, (0.1, 0.1, 0.2)) 

Answer 1

Using the notation in http://www.ccs.neu.edu/home/rplatt/cs5335_fall2017/slides/homogeneous_transforms.pdf, let's say you have 2 Homogeneous Transformation matrices of the objects in the world frame and .
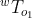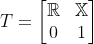You can compose the 4x4 transformation matrices using where R is the 3x3 rotation matrix and X is a 3x1 the translation vector.

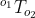What you are looking for is which is simply 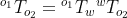where

Once you transform object one in your desired way, you should be able to just apply and get the desired results.

Update:
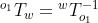
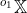If refers to the coordinates of points (for examples object points like its corners) in object 2's local co-orindate system as 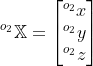. Then these points are given in the any arbitrary frame f as

Here is some code based on your code, hope I understand what you are trying to do:

from tf.transformations import euler_from_quaternion, quaternion_from_euler, \
                               quaternion_matrix, quaternion_from_matrix
from geometry_msgs.msg import PoseStamped, Pose, Point, Quaternion
from std_msgs.msg import Header
import numpy as np

def PoseStamped_2_mat(p):
    q = p.pose.orientation
    pos = p.pose.position
    T = quaternion_matrix([q.x,q.y,q.z,q.w])
    T[:3,3] = np.array([pos.x,pos.y,pos.z])
    return T

def Mat_2_posestamped(m,f_id="test"):
    q = quaternion_from_matrix(m)
    p = PoseStamped(header = Header(frame_id=f_id), #robot.get_planning_frame()
                    pose=Pose(position=Point(*m[:3,3]), 
                    orientation=Quaternion(*q)))
    return p

def T_inv(T_in):
    R_in = T_in[:3,:3]
    t_in = T_in[:3,[-1]]
    R_out = R_in.T
    t_out = -np.matmul(R_out,t_in)
    return np.vstack((np.hstack((R_out,t_out)),np.array([0, 0, 0, 1])))

#This is object2
p_o2 = PoseStamped(header = Header(frame_id="test"), #robot.get_planning_frame()
                   pose=Pose(position=Point(0.9,0.3,1.2), 
                   orientation=Quaternion(0,0,0,1)))

#scene.add_box("object2", p_o2, (0.1, 0.1, 0.2))
#rospy.sleep(2)
Tw2 = PoseStamped_2_mat(p_o2)

#This is object1
p_o1 = PoseStamped(header = Header(frame_id="test"), #robot.get_planning_frame()
                   pose=Pose(position=Point(0.9,0.3,0.7), 
                   orientation=Quaternion(0,0,0,1)))
#scene.add_box("object1", p_o1, (0.1, 0.1, 0.5))
#rospy.sleep(2)
Tw1 = PoseStamped_2_mat(p_o1)

T2w = T_inv(Tw2)
T21 = np.matmul(T2w, Tw1) 

#rospy.sleep(10)
#This is object1 in second pose
p_o2_prime = PoseStamped(header = Header(frame_id="test"), #robot.get_planning_frame()
                         pose=Pose(position=Point(0.7,-0.9,0.7), 
                         orientation=Quaternion(0.3826834,0,0,-0.9238795)))
#scene.add_box("object1", p_o2_prime, (0.1, 0.1, 0.5))
Tw2_prime = PoseStamped_2_mat(p_o2_prime)


Tw1_prime = np.matmul(Tw2_prime, T21)

#rospy.sleep(2)

print "============ Generating plan 2"

#This is object2 in second pose
p_o1_prime = Mat_2_posestamped(Tw1_prime, f_id="test") #  robot.get_planning_frame()
#scene.add_box("object2", p_o1_prime, (0.1, 0.1, 0.2))