3

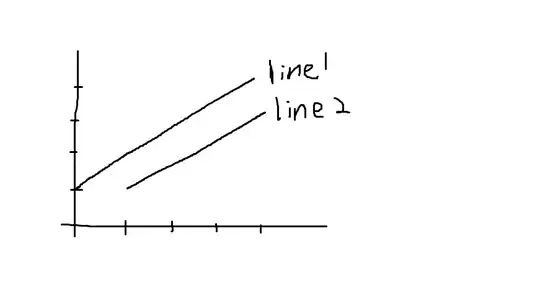
I have some problems with figuring out why you need to revisit all time steps from an episode on each horizon advance for the On-Line version of the λ-return algorithm from the book:
Reinforcement Learning: An Introduction, 2nd Edition, Chapter 12, Sutton & Barto

Horizon step-by-step expansion

Here all sequences of weight vectors W1, W2,..., Wh for each horizon h start from W0(the weights from the end of the previous episode). However they do not seem to depend on the returns/weights from the previous horizon and can be calculated independently. This appears to me explained like that just for clarification and you can calculate them only for the final horizon h=T at episode termination. This will be the same what is done for the Off-line version of the algorithm and the actual update rule is:

General weight-vector update formula

Not surprisingly I get exactly the same results for the 2 algorithms on the 19-states Random Walk example:

On-line VS Off-line graph chart

In the book it is mentioned that the on-line version should perform a little bit better and for that case it should have the same results as the True Online TD(λ). When implementing the latter it really outperforms the off-line version but I can't figure it out for the simple and slow on-line version.

Any suggestions will be appreciated.

Thank you

Community
  • 1
  • 1
xenomeno
  • 63
  • 7

1 Answers1

3

This appears to me explained like that just for clarification and you can calculate them only for the final horizon h=T at episode termination.

This is not true. The whole point of the online λ-return algorithm is that it is online: it makes updates during the episode. This is crucial in the control setting, when actions selected are determined by the current value estimates. Even in the prediction setting, the weight updates made for earlier horizons have an effect.

This is because the final weight vector from the last horizon is always used in the calculation of the update target, the truncated lambda return. So w_1^1 is used to calculate all targets for h=2, and w_2^2 is used to calculate all targets for h=3. Because the targets are calculated using the latest weight vectors, they are generally more accurate.

Even in the prediction setting, the online lambda return algorithm outperforms the offline version because the targets it uses are better.

Philip Raeisghasem
  • 241
  • 1
  • 8
  • @philip_raesghasem You are right that in the control setting it would matter more. In the online version the value estimate is updated towards the same as for the offline one with the only difference being termination time T being replaced with horizon h and at the end is used G{t:h} instead of just Gt. The point I miss is why those updates before the final horizon T would matter if in the book they say a few sentences before your quote: "The first weight vector wh 0 in each sequence is that inherited from the previous episode (so they are the same for all h)" – xenomeno Mar 08 '19 at 19:06
  • Yes, about the more informative updates I agree. I was just wondering why at the end it does not give slightly better results than the offline version as is in the book. Thank you – xenomeno Mar 10 '19 at 16:57
  • @xenomeno, I revisited this problem and realized I was wrong. My edited answer has some concrete changes you should make to your code. – Philip Raeisghasem Apr 14 '19 at 01:49
  • where is w_1^1 used as a target for h=2 or w_2^2 for h=3? For every h: w_0^h is the same initial weight vector(inherited from the previous episode, not horizon) and only w_t^h from the same horizon are used, e.g. they do not rely on the w_t^(h-1) from the previous horizon? – xenomeno Apr 15 '19 at 07:42
  • @xenomeno The target for each update is the truncated lambda return G. See (12.9) and (12.1) for how to compute it. It is ultimately a function of some weights w. The weights you use in calculating G for each horizon h is w_{h-1}^{h-1}. – Philip Raeisghasem Apr 16 '19 at 17:38
  • For anyone reading this now and as confused as I was, the key implicit sentence to me is at top of page 298: "We have new data in the form of R2 and S2, as well as the new w1, so now we can construct a better update target..." – Robin Carter Sep 14 '21 at 20:07