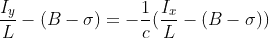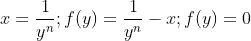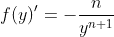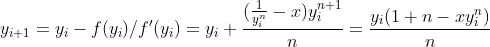The algorithm consists of two steps - a rough solution estimation and the solution improvement using several Newton method steps.
Rough estimation
The basic idea is to use relationship between float number logarithm log2(x) and its integer representation Ix:
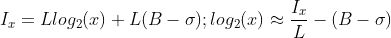
(Image from https://en.wikipedia.org/wiki/Fast_inverse_square_root)
Now use the well-known logarithm identity for root:
![log_{2}(\frac{1}{\sqrt[n]{x}})=-\frac{1}{n}log_{2}(x)](../../images/3123848415.webp) .
.
Combining the identities obtained earlier, we get:
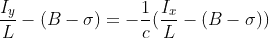

Substituting numerical values L * (B - s) = 0x3F7A3BEA, so
Iy = 0x3F7A3BEA / c * (c + 1) - Ix / c;.
For a simple float point number representation as an integer and back it is convenient to use union type:
union
{
float f; // float representation
uint32_t i; // integer representation
} t;
t.f = x;
t.i = 0x3F7A3BEA / n * (n + 1) - t.i / n; // Work with integer representation
float y = t.f; // back to float representation
Note that for n=2 the expression is simplified to t.i = 0x5f3759df - t.i / 2; which is identical to original i = 0x5f3759df - ( i >> 1 );
Newton's solution improvement
Transform equality
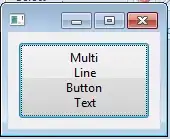
into an equation that should be solved:
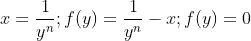
Now construct Newton steps:
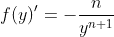
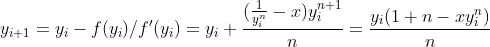
Programmatically it looks like: y = y * (1 + n - x * pow(y,n)) / n;. As an initial y, we use the value obtained at Rough estimation step.
Note for the particular case of square root (n = 2) we get y = y * (3 - x*y*y) / 2; which is identically to the original formula y = y * (threehalfs - (x2 * y * y));
Final code as template function. Parameter N determines root power.
template<unsigned N>
float power(float x) {
if (N % 2 == 0) return power<N / 2>(x * x);
else if (N % 3 == 0) return power<N / 3>(x * x * x);
return power<N - 1>(x) * x;
};
template<>
float power<0>(float x){ return 1; }
// fast_inv_nth_root<2>(x) - inverse square root 1/sqrt(x)
// fast_inv_nth_root<3>(x) - inverse cube root 1/cbrt(x)
template <unsigned n>
float fast_inv_nth_root(float x)
{
union { float f; uint32_t i; } t = { x };
// Approximate solution
t.i = 0x3F7A3BEA / n * (n + 1) - t.i / n;
float y = t.f;
// Newton's steps. Copy for more accuracy.
y = y * (n + 1 - x * power<n>(y)) / n;
y = y * (n + 1 - x * power<n>(y)) / n;
return y;
}
Testing
Testing code:
int main()
{
std::cout << "|x ""|fast2 "" actual2 "
"|fast3 "" actual3 "
"|fast4 "" actual4 "
"|fast5 "" actual5 ""|" << std::endl;
for (float i = 0.00001; i < 10000; i *= 10)
std::cout << std::setprecision(5) << std::fixed
<< std::scientific << '|'
<< i << '|'
<< fast_inv_nth_root<2>(i) << " " << 1 / sqrt(i) << "|"
<< fast_inv_nth_root<3>(i) << " " << 1 / cbrt(i) << "|"
<< fast_inv_nth_root<4>(i) << " " << pow(i, -0.25) << "|"
<< fast_inv_nth_root<5>(i) << " " << pow(i, -0.2) << "|"
<< std::endl;
}
Results:
|x |fast2 actual2 |fast3 actual3 |fast4 actual4 |fast5 actual5 |
|1.00000e-05|3.16226e+02 3.16228e+02|4.64152e+01 4.64159e+01|1.77828e+01 1.77828e+01|9.99985e+00 1.00000e+01|
|1.00000e-04|9.99996e+01 1.00000e+02|2.15441e+01 2.15443e+01|9.99991e+00 1.00000e+01|6.30949e+00 6.30957e+00|
|1.00000e-03|3.16227e+01 3.16228e+01|1.00000e+01 1.00000e+01|5.62339e+00 5.62341e+00|3.98103e+00 3.98107e+00|
|1.00000e-02|9.99995e+00 1.00000e+01|4.64159e+00 4.64159e+00|3.16225e+00 3.16228e+00|2.51185e+00 2.51189e+00|
|1.00000e-01|3.16227e+00 3.16228e+00|2.15443e+00 2.15443e+00|1.77828e+00 1.77828e+00|1.58487e+00 1.58489e+00|
|1.00000e+00|9.99996e-01 1.00000e+00|9.99994e-01 1.00000e+00|9.99991e-01 1.00000e+00|9.99987e-01 1.00000e+00|
|1.00000e+01|3.16226e-01 3.16228e-01|4.64159e-01 4.64159e-01|5.62341e-01 5.62341e-01|6.30948e-01 6.30957e-01|
|1.00000e+02|9.99997e-02 1.00000e-01|2.15443e-01 2.15443e-01|3.16223e-01 3.16228e-01|3.98102e-01 3.98107e-01|
|1.00000e+03|3.16226e-02 3.16228e-02|1.00000e-01 1.00000e-01|1.77827e-01 1.77828e-01|2.51185e-01 2.51189e-01|
|1.00000e+04|9.99996e-03 1.00000e-02|4.64155e-02 4.64159e-02|9.99995e-02 1.00000e-01|1.58487e-01 1.58489e-01|
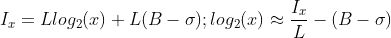

![log_{2}(\frac{1}{\sqrt[n]{x}})=-\frac{1}{n}log_{2}(x)](../../images/3123848415.webp) .
.