Sympy - Rename part of an expression

Question

Say I have defined the following expression:

from sympy import *
N, D, i, j, d = symbols("N D i j d", integer=True)
beta, gamma = symbols(r'\beta \gamma')
X = IndexedBase("X", shape=(N, D))

# r(i, j) = euclidian distance between X[i] and X[j]
r = lambda i, j: sqrt(Sum((X[i, d] - X[j, d])**2, (d, 1, D)))
expr = r(i, j)**2 + r(i, j)

The expr variable now displays like this:

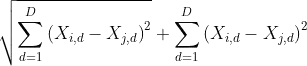
$\sqrt{\sum_{d=1}^{D} \left({X}_{i,d} - {X}_{j,d}\right)^{2}} + \sum_{d=1}^{D} \left({X}_{i,d} - {X}_{j,d}\right)^{2}$

While this is fine for this minimal example, it gets quite messy in larger expressions. This really hinders my ability to see what happens later on when I compute sums over all r(i,j), derivatives etc.

My question: Is there a way to tell SymPy about r(i, j), such that it can be displayed as something like this:

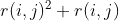
r(i,j)^2+r(i,j)

while still behaving as before in subsequent expressions?

I know I could make r a Function, which would display as wanted, but then it would not work properly in a subsequent calculation (e.g. derivatives would be abstract and not evaluated).

Any help would be much appreciated!

I'm not too familiar with Sympy, is this helpful at all: (https://docs.sympy.org/latest/modules/rewriting.html)? — OrderAndChaos, Mar 08 '19 at 07:22
@Sarcoma Didn't know about that, nice! With `cse` it's able to auto-replace the common subexpressions, which is nice. But it's still not a full solution, as the resulting expressions "forget" their origin, and e.g. derivatives don't work as they should. I tried taking the derivative first, then `cse`, but then it tends to find other patterns than what I would expect it to. — Bendik, Mar 08 '19 at 07:47
What do you mean derivatives would be abstract and not evaluated? — ALFA, Mar 08 '19 at 11:44
@ALFA I mean that `diff(r(i,j), X[k,l])` evaluates to zero because there is no known dependency on `X` within the function `r` (if I define `r` as a `Function` symbol). The only derivatives that make sense for SymPy is `diff(r(i,j), i, 1)` (or same with `j`), which would not be able to evaluate to anything (it's just the derivative of some function), plus not being very relevant in this case. — Bendik, Mar 08 '19 at 11:51
I did manage to get something working following the examples in https://docs.sympy.org/latest/modules/printing.html#example-of-custom-printing-method on some built in functions. It didn't seem to work nicely with my custom class. I'll play around with it a bit more. — OrderAndChaos, Mar 08 '19 at 12:36
@ALFA I've have asked a new question about how to customise the output of a `Function` class. https://stackoverflow.com/questions/55070462/sympy-custom-print-format-for-a-custom-function-expression. — OrderAndChaos, Mar 08 '19 at 20:21

score 2 · Answer 1 · answered Mar 08 '19 at 12:06

2

I don't really know if it may helps you but what about this:

from sympy import *
from sympy.utilities.lambdify import lambdify, implemented_function
N, D, i, j, d = symbols("N D i j d", integer=True)
beta, gamma = symbols(r'\beta \gamma')
X = IndexedBase("X", shape=(N, D))

r = implemented_function('r', lambda i, j: sqrt(Sum((X[i, d] - X[j, d])**2, (d, 1, D))));
expr = r(i, j)**2 + r(i, j)
print(expr)
r = lambdify((i,j), r(i,j))
print(diff(r(i,j), X[i,j]))

You can display your expression as you wish, then use lambdify() and makes it behave as it should. Just guessing, maybe it's useless for you as you probably prefer a way to maintain the same expression all along the code.

answered Mar 08 '19 at 12:06

ALFA

1,726
1
10
19

I'd come across this, looked like it ought to do the trick. Couldn't get it working though. I saw this in the docs for lambdify: "Be aware that this is a quick workaround, not a general method to create special symbolic functions. If you want to create a symbolic function to be used by all the machinery of SymPy you should subclass the Function class." which led me to think that the more verbose `class r(Function):` might also work. – OrderAndChaos Mar 08 '19 at 12:21
That's pretty close actually. It's slightly awkward to have to change between the two all the time, but still. With `r_func = lambdify((i,j), r(i,j)) ` defined and doing `diff(expr.subs(r(i,j), r_func(i,j)), X[k,l]).subs(r_func(i,j), r(i,j))` it works the way I want it to. Wrapping this whole thing in `cse` makes it even simpler. – Bendik Mar 08 '19 at 12:24
1

@Sarcoma But perhaps the `Function` subclass is the way to go to make this "smoother", although more work upfront... I'm gonna tinker with it a bit – Bendik Mar 08 '19 at 12:26
1

Yes I would implement this with Function subclass. I think this is the closest option to your request, doing further researches on the web l could’t find a better way – ALFA Mar 08 '19 at 13:59

score 2 · Accepted Answer · answered Mar 08 '19 at 22:44

You can make a custom Function subclass that doesn't evaluate by default:

class r(Function):
    @classmethod
    def eval(cls, i, j):
        return

    def doit(self, **kwargs):
        i, j = self.args
        return sqrt(Sum((X[i, d] - X[j, d])**2, (d, 1, D)))

eval tells it when to evaluate. Since it always returns None, it never evaluates. It also tells SymPy the function has two arguments. You can also have it return explicit values in some cases, if you like. For instance, you might want it to evaluate if i and j are explicit numbers.

@classmethod
def eval(cls, i, j):
    if i.is_Number and j.is_Number:
        return sqrt(Sum((X[i, d] - X[j, d])**2, (d, 1, D)))

With this you can use it as desired, and call expr.doit() when you want it to evaluate. You can also specifically define evaluation for certain functions to avoid doit. For example, derivatives:

def _eval_derivative(self, x):
    return self.doit()._eval_derivative(x)

This will make r(i, j).diff(i) evaluate immediately without having to call doit.

Other functions have similar methods you can define. See the SymPy documentation.

Sympy - Rename part of an expression

2 Answers2