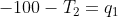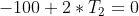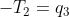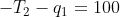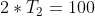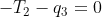Solving a linear system of equations

Question

I am working on using the finite element method to calculate heat flow through elements. I'm currently stuck on solving a system of equations where there is variables on both side of the equality. A simple example could be something like this

| 1  -1   0|   |100 |   |q1|   
|-1   2  -1| . | T2 | = |0 |   
| 0  -1   1|   | 0  |   |q3|

The method I'm thinking about using would reduce the matrix to a 2x2 as the temperature "T1" is known and change the right hand side accordingly. And continue by doing the same in the row of "T3". However my counselor have been advising me agianst this.

How would you go about solving a system like this?

Sounds like you're confused about how to apply Dirchelet boundary conditions. You will only have unknown temperatures to solve for if you do it correctly. https://scicomp.stackexchange.com/questions/11531/fem-which-is-the-correct-way-to-impose-dirichlet-b-c — duffymo, Mar 03 '23 at 14:32

Freakazoid · Answer 1 · 2019-02-25T07:31:31.637

2

I would write down your linear equations and reshape it, such that you have only one vector with unknown variables. For example, your equations system from above are equal to:

which can be rewritten:

which yields to:

| -1  -1   0|   | T2 |   | 100 |   
|  2   0   0| . | q1 | = | 100 |   
| -1   0  -1|   | q3 |   |  0  |

edited Feb 25 '19 at 07:31

answered Feb 22 '19 at 10:55

Freakazoid

490
3
10

1

Thanks that helps,100 should just be moved to the right hand side, then numpy.linalg.solve can do the rest. – Jonas Jacobsen Feb 22 '19 at 13:45

score 2 · Accepted Answer · edited Feb 23 '23 at 23:07

Another way to do this is to create a permutation matrix to extract known and unknown rows out of your vectors. This method is a little more complicated, but much more programmer friendly:

Say your eq. system is:

K . T = Q

where K is 3x3, and T and Q are 3x1 vectors. You can create a permutation Pf matrix in a way that when it multiplied by T, result is unknown part of T matrix (which is only T2), in your case permutation matrix will be a 1x3 matrix:

Pf = [0 1 0]

                       |100|
Tf = Pf * T = [0 1 0]* |T2 | = [T2]
                       |0  |

another permutation matrix will gets the known part out of T matrix, in your case it will be a 2x3 matrix:

     | 1 0 0|
Ps = | 0 0 1| 

Ts =  Ps * T = | 1 0 0|  |100|   |100|
               | 0 0 1| *| T2| = |0  |
                         |0  |

Now everything is ready, you can assume the system like this:

K . T = Q

K = |Kff Kfs|
    |Ksf Kss|

Q = |Qf|
    |Qs|

T = |Tf|
    |Ts|

where f is prefix for unknown right side, and s prefix is for known right side. you can find Pf, Ps, Qf, Qs, Kff, Kfs, Ksf and Kss like this:

Tf = Pf * T
Ts = Ps * T

Qf = Pf * Q
Qs = Ps * Q

Kff = pf * K * pf` (note: ` denotes the transpose)
Kfs = pf * K * ps` (note: ` denotes the transpose)
Ksf = ps * K * pf` (note: ` denotes the transpose)
Kss = ps * K * ps` (note: ` denotes the transpose)

now unknown vectors Tf and Qs needs to be found:

K . T = Q

|Kff Kfs| |Tf| = |Qf|
|Ksf Kss| |Ts|   |Qs|

means that:

Kff * Tf + Kfs * Ts = Qf
Ksf * Tf + Kss * Ts = Qs

from first one:

Tf = Kff^-1 * (Qf - Kfs * Ts)

with above equation you can find Tf (note that all right sides are known matrix and vectors, so numeric operations need to be performed)

and from second one:

Qs = Ksf * Tf + Kss * Ts

this way both Qs and Tf are found. Once you found Tf and Qs, you can do this to form original T and Q matrix:

Q = Ps` * Qs + Pf` * Qf
T = Ps` * Ts + Pf` * Tf

Thank you so much for taking your time to answer. This was exactly what my partner and I were looking for! We had found this method in our study book but was having a hard time wrapping our head around it. This is a much better explanation, thank you! — Jonas Jacobsen, Feb 25 '19 at 14:44
@JonasJacobsen you noted that you have seen this method in another textbook, can you please tell me the name of the book? thanks — epsi1on, Dec 15 '19 at 06:09

Solving a linear system of equations

2 Answers2