Pytorch: How to create an update rule that doesn't come from derivatives?

Question

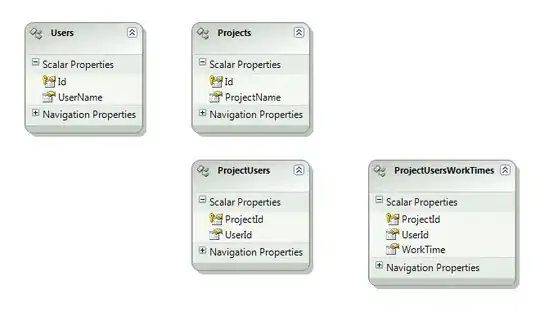
I want to implement the following algorithm, taken from this book, section 13.6:

I don't understand how to implement the update rule in pytorch (the rule for w is quite similar to that of theta).

As far as I know, torch requires a loss for loss.backwward().

This form does not seem to apply for the quoted algorithm.

I'm still certain there is a correct way of implementing such update rules in pytorch.

Would greatly appreciate a code snippet of how the w weights should be updated, given that V(s,w) is the output of the neural net, parameterized by w.

EDIT: Chris Holland suggested a way to implement, and I implemented it. It does not converge on Cartpole, and I wonder if I did something wrong.

The critic does converge on the solution to the function gamma*f(n)=f(n)-1 which happens to be the sum of the series gamma+gamma^2+...+gamma^inf meaning, gamma=1 diverges. gamma=0.99 converges on 100, gamma=0.5 converges on 2 and so on. Regardless of the actor or policy.

The code:

def _update_grads_with_eligibility(self, is_critic, delta, discount, ep_t):
    gamma = self.args.gamma
    if is_critic:
        params = list(self.critic_nn.parameters())
        lamb = self.critic_lambda
        eligibilities = self.critic_eligibilities
    else:
        params = list(self.actor_nn.parameters())
        lamb = self.actor_lambda
        eligibilities = self.actor_eligibilities

    is_episode_just_started = (ep_t == 0)
    if is_episode_just_started:
        eligibilities.clear()
        for i, p in enumerate(params):
            if not p.requires_grad:
                continue
            eligibilities.append(torch.zeros_like(p.grad, requires_grad=False))

    # eligibility traces
    for i, p in enumerate(params):

        if not p.requires_grad:
            continue
        eligibilities[i][:] = (gamma * lamb * eligibilities[i]) + (discount * p.grad)
        p.grad[:] = delta.squeeze() * eligibilities[i]

and

expected_reward_from_t = self.critic_nn(s_t)
probs_t = self.actor_nn(s_t)
expected_reward_from_t1 = torch.tensor([[0]], dtype=torch.float)
if s_t1 is not None:  # s_t is not a terminal state, s_t1 exists.
    expected_reward_from_t1 = self.critic_nn(s_t1)

delta = r_t + gamma * expected_reward_from_t1.data - expected_reward_from_t.data

negative_expected_reward_from_t = -expected_reward_from_t
self.critic_optimizer.zero_grad()
negative_expected_reward_from_t.backward()
self._update_grads_with_eligibility(is_critic=True,
                                    delta=delta,
                                    discount=discount,
                                    ep_t=ep_t)
self.critic_optimizer.step()

EDIT 2: Chris Holland's solution works. The problem originated from a bug in my code that caused the line

if s_t1 is not None:
    expected_reward_from_t1 = self.critic_nn(s_t1)

to always get called, thus expected_reward_from_t1 was never zero, and thus no stopping condition was specified for the bellman equation recursion.

With no reward engineering, gamma=1, lambda=0.6, and a single hidden layer of size 128 for both actor and critic, this converged on a rather stable optimal policy within 500 episodes.

Even faster with gamma=0.99, as the graph shows (best discounted episode reward is about 86.6).

BIG thank you to @Chris Holland, who "gave this a try"

Note that the linked book draft as well as the screenshot apparently contain an error, namely the trace update for the value function should not contain the running discount factor `I` (i.e. `gamma**t`), as can be seen from the chapter about eligibility traces. Also in the final second edition of the book this has been corrected. — a_guest, Feb 21 '19 at 20:26
@a_guest could you link to the corrected version please? What is the correct formula then, and why does this one work? — Gulzar, Feb 21 '19 at 21:06
The second edition can be found [here](http://www.incompleteideas.net/book/RLbook2018trimmed.pdf). If gamma is close to one there won't be a big difference and for smaller value of gamma the effect is basically that the updates are decreased with the episode's steps, i.e. learning towards the end of an episode is slowed down (since new gradients don't really add to the already decayed ones). This modifies the trace but perhaps doesn't prevent the algorithm from learning, it probably just takes more time to do so. — a_guest, Feb 21 '19 at 21:14
Thanks! Do you know why the critic doesn't have that discount and the actor does? — Gulzar, Feb 21 '19 at 21:21
In general eligibility traces don't have that accumulated discount since it would conflict with the definition of discounted return. The actor trace on the other hand does have this additional discount since the policy gradient method uses the value function of the *initial* state as a performance metric (see eq. (13.4) in the 2nd ed.). The policy's gradient is then derived to be proportional to that metric (eq. (13.5)). Hence all corresponding updates need to be properly discounted with respect to that initial state (initial step), hence the additional `gamma**t` factor. — a_guest, Feb 21 '19 at 21:34
Can this algorithm be converted into one in which we only call `.backward()` on a single scalar value on each iteration, letting the `optimizer.step()` take care of updating the parameters? — user76284, Oct 12 '20 at 07:50
@user76284 I think that may have been a better phrasing for my original question, and if you find a way, I will be more than happy to know. — Gulzar, Oct 12 '20 at 07:52
Will do. Also, which lambda values did you use for your final cartpole result? — user76284, Oct 12 '20 at 08:03

Chris Holland · Accepted Answer · 2019-02-21T15:27:48.157

6

I am gonna give this a try.

.backward() does not need a loss function, it just needs a differentiable scalar output. It approximates a gradient with respect to the model parameters. Let's just look at the first case the update for the value function.

We have one gradient appearing for v, we can approximate this gradient by

v = model(s)
v.backward()

This gives us a gradient of v which has the dimension of your model parameters. Assuming we already calculated the other parameter updates, we can calculate the actual optimizer update:

for i, p in enumerate(model.parameters()):
    z_theta[i][:] = gamma * lamda * z_theta[i] + l * p.grad
    p.grad[:] = alpha * delta * z_theta[i]

We can then use opt.step() to update the model parameters with the adjusted gradient.

edited Feb 21 '19 at 15:27

answered Feb 18 '19 at 16:49

Chris Holland

559
4
11

Thanks! will try this right away! just a question: How would z_theta be initialized? So far I have been getting an anoying `output with shape [1] doesn't match the broadcast shape [1, 1]` and I bet I am not initializing correctly. – Gulzar Feb 18 '19 at 17:09
According to your picture z_theta is initialized with 0, which would have to be in the same shape as your model paramers. So one way would be something like `with torch.no_grad(): z_theta = [p*0 for p in model.parameters()]` – Chris Holland Feb 18 '19 at 17:27
Just to make sure - `p.grad() = alpha * delta * z_theta[i]` alpha shouldn't be there, right? It is the learning rate, and comes build into the optimizer. Did I get it wrong? Also, Is there any difference between a weight parameter and a bias parameter? – Gulzar Feb 18 '19 at 22:42
So I implemented the code as you suggested. It doesn't converge on Cartpole, which is unexpected. Worse, if I set the actor to learn nothing, just the critic doesn't even converge on the correct value function of the static policy. I am kind of clueless about how to debug this... I added the full code as an edit to the original question – Gulzar Feb 20 '19 at 22:03
Can this algorithm be converted into one in which we only call `.backward()` on a single scalar value on each iteration, letting the `optimizer.step()` take care of updating the parameters? – user76284 Oct 12 '20 at 07:52
@user76284 The point of this question is I found no such way. If you are aware of one, please do post it. – Gulzar Apr 12 '21 at 19:18

Pytorch: How to create an update rule that doesn't come from derivatives?

1 Answers1

Linked