I have 4 points.. i can draw a polygon usign this code
var p = new Polygon();
p.Points.Add(new Point(0, 0));
p.Points.Add(new Point(70, 0));
p.Points.Add(new Point(90, 100));
p.Points.Add(new Point(0, 80));
How i can draw an 'ellipse' that will fit in this polygon, using Silverlight?
One way is use QuadraticBezierSegment or BezierSegment.
For example, like this:
<Path Stroke="Red" StrokeThickness="2" >
<Path.Data>
<PathGeometry>
<PathGeometry.Figures>
<PathFigureCollection>
<PathFigure StartPoint="0,40">
<PathFigure.Segments>
<PathSegmentCollection>
<BezierSegment Point1="0,93"
Point2="90,117"
Point3="80,50"
/>
</PathSegmentCollection>
</PathFigure.Segments>
</PathFigure>
</PathFigureCollection>
</PathGeometry.Figures>
</PathGeometry>
</Path.Data>
</Path>
<Path Stroke="Red" StrokeThickness="2" >
<Path.Data>
<PathGeometry>
<PathGeometry.Figures>
<PathFigureCollection>
<PathFigure StartPoint="0,40">
<PathFigure.Segments>
<PathSegmentCollection>
<BezierSegment Point1="0,-13"
Point2="70,-17"
Point3="80,50"
/>
</PathSegmentCollection>
</PathFigure.Segments>
</PathFigure>
</PathFigureCollection>
</PathGeometry.Figures>
</PathGeometry>
</Path.Data>
</Path>
<Polygon Points="0,0 70,0 90,100 0,80"></Polygon>
it's not exact solution, for exact you must colculate exact points for curves and use 4 QuadraticBezierSegment
Edit:
Example for QuadraticBezierSegment
<Path Stroke="Red" StrokeThickness="1">
<Path.Data>
<PathGeometry>
<PathGeometry.Figures>
<PathFigureCollection>
<PathFigure StartPoint="0,40">
<PathFigure.Segments>
<PathSegmentCollection>
<QuadraticBezierSegment Point1="6,79"
Point2="45,90"
/>
</PathSegmentCollection>
</PathFigure.Segments>
</PathFigure>
</PathFigureCollection>
</PathGeometry.Figures>
</PathGeometry>
</Path.Data>
</Path>
<Path Stroke="Red" StrokeThickness="1">
<Path.Data>
<PathGeometry>
<PathGeometry.Figures>
<PathFigureCollection>
<PathFigure StartPoint="45,90">
<PathFigure.Segments>
<PathSegmentCollection>
<QuadraticBezierSegment Point1="80,91"
Point2="80,50"
/>
</PathSegmentCollection>
</PathFigure.Segments>
</PathFigure>
</PathFigureCollection>
</PathGeometry.Figures>
</PathGeometry>
</Path.Data>
</Path>
<Path Stroke="Red" StrokeThickness="1">
<Path.Data>
<PathGeometry>
<PathGeometry.Figures>
<PathFigureCollection>
<PathFigure StartPoint="0,40">
<PathFigure.Segments>
<PathSegmentCollection>
<QuadraticBezierSegment Point1="2,3"
Point2="35,0"
/>
</PathSegmentCollection>
</PathFigure.Segments>
</PathFigure>
</PathFigureCollection>
</PathGeometry.Figures>
</PathGeometry>
</Path.Data>
</Path>
<Path Stroke="Red" StrokeThickness="1">
<Path.Data>
<PathGeometry>
<PathGeometry.Figures>
<PathFigureCollection>
<PathFigure StartPoint="35,0">
<PathFigure.Segments>
<PathSegmentCollection>
<QuadraticBezierSegment Point1="72,8"
Point2="80,50"
/>
</PathSegmentCollection>
</PathFigure.Segments>
</PathFigure>
</PathFigureCollection>
</PathGeometry.Figures>
</PathGeometry>
</Path.Data>
</Path>
<Polygon Name="pol" Points="0,0 70,0 90,100 0,80" Stroke="Red" StrokeThickness="1"</Polygon>
it still an experimental, not calculate point, but it quite exact.
Edit2: You may calculate points of curves with use of this image and my comments:
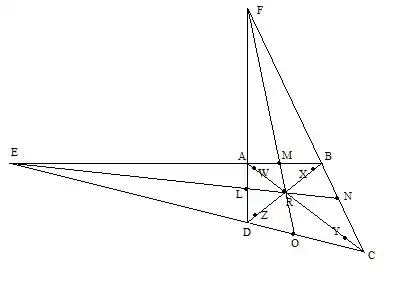
curves have a startpoint, midle point and endpoint. In this image start and end piont are L,M,N,O; and midle are W,X,Y,Z.
How for example we calculate point L:
Whith help of equation of line y = k * x + b we find equation of line AB,DC,AC,DB,AD. How cross of AC and DB we find R. How cross of AB and DC we find E. After that we find equation of line ER and how cross of ER and AD we find L.
How we calculate point W:
Whith help of equation for length l = sqrt(sqr(x2 - x1) + sqr(y2 - y1)) find length of AR. AW = AR/(4*pi) and whith help of this coefficient, and equation of line and equation for length, after solving of square equation we find W.
Other points we find similarly.
This algorithm not work only for polygon which have parallel line, but in this case algorithm is more easier. And coefficient for length are the same.
Whith help of this algorithm i find point for 3 curves of your example:
<Path Stroke="Red" StrokeThickness="1">
<Path.Data>
<PathGeometry>
<PathGeometry.Figures>
<PathFigureCollection>
<PathFigure StartPoint="0,36">
<PathFigure.Segments>
<PathSegmentCollection>
<QuadraticBezierSegment Point1="4.7,74.6"
Point2="39.9,88.9"
/>
</PathSegmentCollection>
</PathFigure.Segments>
</PathFigure>
</PathFigureCollection>
</PathGeometry.Figures>
</PathGeometry>
</Path.Data>
</Path>
<Path Stroke="Red" StrokeThickness="1">
<Path.Data>
<PathGeometry>
<PathGeometry.Figures>
<PathFigureCollection>
<PathFigure StartPoint="39.9,88.9">
<PathFigure.Segments>
<PathSegmentCollection>
<QuadraticBezierSegment Point1="83.43,92.7"
Point2="78.8,43.9"
/>
</PathSegmentCollection>
</PathFigure.Segments>
</PathFigure>
</PathFigureCollection>
</PathGeometry.Figures>
</PathGeometry>
</Path.Data>
</Path>
<Path Stroke="Red" StrokeThickness="1">
<Path.Data>
<PathGeometry>
<PathGeometry.Figures>
<PathFigureCollection>
<PathFigure StartPoint="0,36">
<PathFigure.Segments>
<PathSegmentCollection>
<QuadraticBezierSegment Point1="3.55,3.94"
Point2="31.8,0"
/>
</PathSegmentCollection>
</PathFigure.Segments>
</PathFigure>
</PathFigureCollection>
</PathGeometry.Figures>
</PathGeometry>
</Path.Data>
</Path>
And it curves exactly the same as ellipse line. Image below:
You may translate this algorithm to 'formula' and so find your solution.
You need 4 function for that:
1) find line coefficients from coordinates of 2 pionts
2) find coordinates of piont how cross of 2 lines from it's coefficients
3) find length of segment from coordinates of 2 points
4) find coordinates of piont whiсh lies on line with this start point and this length from line coefficients and coordinates of start point and length which you find in previous function divided by (4*pi)
Edit3: You may optimize this solution, it have some defects, how parallel line etc. But it fast and if you optimise it may satisfy your requirements.
Xaml:
<Path Stroke="Red" StrokeThickness="1">
<Path.Data>
<PathGeometry>
<PathGeometry.Figures>
<PathFigureCollection>
<PathFigure x:Name="pathleftdown" StartPoint="0,0">
<PathFigure.Segments>
<PathSegmentCollection>
<QuadraticBezierSegment x:Name="bezleftdown" Point1="0,0"
Point2="0,0"
/>
</PathSegmentCollection>
</PathFigure.Segments>
</PathFigure>
</PathFigureCollection>
</PathGeometry.Figures>
</PathGeometry>
</Path.Data>
</Path>
<Path Stroke="Red" StrokeThickness="1">
<Path.Data>
<PathGeometry>
<PathGeometry.Figures>
<PathFigureCollection>
<PathFigure x:Name="pathrigthdown" StartPoint="0,0">
<PathFigure.Segments>
<PathSegmentCollection>
<QuadraticBezierSegment x:Name="bezrigthdown" Point1="0,0"
Point2="0,0"
/>
</PathSegmentCollection>
</PathFigure.Segments>
</PathFigure>
</PathFigureCollection>
</PathGeometry.Figures>
</PathGeometry>
</Path.Data>
</Path>
<Path Stroke="Red" StrokeThickness="1">
<Path.Data>
<PathGeometry>
<PathGeometry.Figures>
<PathFigureCollection>
<PathFigure x:Name="pathleftup" StartPoint="0,0">
<PathFigure.Segments>
<PathSegmentCollection>
<QuadraticBezierSegment x:Name="bezleftup" Point1="0,0"
Point2="0,0"
/>
</PathSegmentCollection>
</PathFigure.Segments>
</PathFigure>
</PathFigureCollection>
</PathGeometry.Figures>
</PathGeometry>
</Path.Data>
</Path>
<Path Stroke="Red" StrokeThickness="1">
<Path.Data>
<PathGeometry>
<PathGeometry.Figures>
<PathFigureCollection>
<PathFigure x:Name="pathrigthup" StartPoint="0,0">
<PathFigure.Segments>
<PathSegmentCollection>
<QuadraticBezierSegment x:Name="bezrigthup" Point1="0,0"
Point2="0,0"
/>
</PathSegmentCollection>
</PathFigure.Segments>
</PathFigure>
</PathFigureCollection>
</PathGeometry.Figures>
</PathGeometry>
</Path.Data>
</Path>
<Polygon Name="pol" Points="0,0 250,0 251,340 0,341" Stroke="Red" StrokeThickness="1"></Polygon>
<Button Content="Generate" Width ="80" Height="30" HorizontalAlignment="Right" VerticalAlignment="Top" Click="Button_Click"></Button>
and code:
private class pointXY
{
public double x;
public double y;
}
private class lineKB
{
public double k;
public double b;
public bool flagXconst = false;
public double xConst = 0;
}
private lineKB GetLineFromPonts(pointXY A, pointXY B)
{
lineKB line = new lineKB();
if ((B.x - A.x) != 0)
{
line.k = (B.y - A.y) / (B.x - A.x);
line.b = A.y - A.x * line.k;
}
else
{
line.xConst = A.x;
line.flagXconst = true;
}
return line;
}
private pointXY GetPointFromLines(lineKB a, lineKB b)
{
pointXY point = new pointXY();
if (a.flagXconst)
{
point.x = a.xConst;
point.y = a.xConst * b.k + b.b;
}else
if (b.flagXconst)
{
point.x = b.xConst;
point.y = b.xConst * a.k + a.b;
}
else
{
point.x = (a.b - b.b) / (b.k - a.k);
point.y = a.k * point.x + a.b;
}
return point;
}
private double LengthOfLine(pointXY A, pointXY B)
{
return Math.Sqrt((B.x - A.x) * (B.x - A.x) + (B.y - A.y) * (B.y - A.y));
}
private pointXY GetMidlePoint(pointXY S, double l, lineKB line, bool leftright)
{
double b = -2 * S.x - 2 * line.k * (-line.b + S.y);
double a = (1 + line.k * line.k);
double c = (S.x * S.x - l * l + (-line.b + S.y) * (-line.b + S.y));
double d = b*b - 4 * a * c;
double x1 = (-b + Math.Sqrt(d)) / (2 * a);
double x2 = (-b - Math.Sqrt(d)) / (2 * a);
pointXY ret = new pointXY();
if (leftright)
if (x1 > S.x) ret.x = x1;
else ret.x = x2;
else
if (x1 < S.x) ret.x = x1;
else ret.x = x2;
ret.y = line.k * ret.x + line.b;
return ret;
}
private void Button_Click(object sender, RoutedEventArgs e)
{
pointXY A = new pointXY();
A.x = pol.Points[0].X;
A.y = pol.Points[0].Y;
pointXY B = new pointXY();
B.x = pol.Points[1].X;
B.y = pol.Points[1].Y;
pointXY C = new pointXY();
C.x = pol.Points[2].X;
C.y = pol.Points[2].Y;
pointXY D = new pointXY();
D.x = pol.Points[3].X;
D.y = pol.Points[3].Y;
lineKB AC = GetLineFromPonts(A, C);
lineKB BD = GetLineFromPonts(B, D);
pointXY R = GetPointFromLines(AC, BD);
lineKB AB = GetLineFromPonts(A, B);
lineKB BC = GetLineFromPonts(B, C);
lineKB CD = GetLineFromPonts(C, D);
lineKB DA = GetLineFromPonts(D, A);
pointXY E = GetPointFromLines(AB, CD);
lineKB ER = GetLineFromPonts(E, R);
pointXY L = GetPointFromLines(ER, DA);
pointXY N = GetPointFromLines(ER, BC);
pointXY F = GetPointFromLines(BC, DA);
lineKB FR = GetLineFromPonts(F, R);
pointXY M = GetPointFromLines(FR, AB);
pointXY O = GetPointFromLines(FR, CD);
pointXY W = GetMidlePoint(A, (LengthOfLine(A, R) / (4 * Math.PI)), AC, true);
pointXY X = GetMidlePoint(B, (LengthOfLine(B, R) / (4 * Math.PI)), BD, false);
pointXY Y = GetMidlePoint(C, (LengthOfLine(C, R) / (4 * Math.PI)), AC, false);
pointXY Z = GetMidlePoint(D, (LengthOfLine(D, R) / (4 * Math.PI)), BD, true);
pathleftup.StartPoint = new Point(L.x, L.y);
bezleftup.Point1 = new Point(W.x, W.y);
bezleftup.Point2 = new Point(M.x, M.y);
pathleftdown.StartPoint = new Point(L.x, L.y);
bezleftdown.Point1 = new Point(Z.x, Z.y);
bezleftdown.Point2 = new Point(O.x, O.y);
pathrigthdown.StartPoint = new Point(O.x, O.y);
bezrigthdown.Point1 = new Point(Y.x, Y.y);
bezrigthdown.Point2 = new Point(N.x, N.y);
pathrigthup.StartPoint = new Point(M.x, M.y);
bezrigthup.Point1 = new Point(X.x, X.y);
bezrigthup.Point2 = new Point(N.x, N.y);
}
With the information given by Jeff M I created a function that returns an ellipse fitting in a polygon:
Ellipse FitEllipse(Polygon poly)
{
double W0 = poly.Points[0].X;
double W1 = poly.Points[0].Y;
double X0 = poly.Points[1].X;
double X1 = poly.Points[1].Y;
double Y0 = poly.Points[2].X;
double Y1 = poly.Points[2].Y;
double Z0 = poly.Points[3].X;
double Z1 = poly.Points[3].Y;
double A = X0 * Y0 * Z1 - W0 * Y0 * Z1 - X0 * Y1 * Z0 + W0 * Y1 * Z0 - W0 * X1 * Z0 + W1 * X0 * Z0 + W0 * X1 * Y0 - W1 * X0 * Y0;
double B = W0 * Y0 * Z1 - W0 * X0 * Z1 - X0 * Y1 * Z0 + X1 * Y0 * Z0 - W1 * Y0 * Z0 + W1 * X0 * Z0 + W0 * X0 * Y1 - W0 * X1 * Y0;
double C = X0 * Y0 * Z1 - W0 * X0 * Z1 - W0 * Y1 * Z0 - X1 * Y0 * Z0 + W1 * Y0 * Z0 + W0 * X1 * Z0 + W0 * X0 * Y1 - W1 * X0 * Y0;
double D = X1 * Y0 * Z1 - W1 * Y0 * Z1 - W0 * X1 * Z1 + W1 * X0 * Z1 - X1 * Y1 * Z0 + W1 * Y1 * Z0 + W0 * X1 * Y1 - W1 * X0 * Y1;
double E = -X0 * Y1 * Z1 + W0 * Y1 * Z1 + X1 * Y0 * Z1 - W0 * X1 * Z1 - W1 * Y1 * Z0 + W1 * X1 * Z0 + W1 * X0 * Y1 - W1 * X1 * Y0;
double F = X0 * Y1 * Z1 - W0 * Y1 * Z1 + W1 * Y0 * Z1 - W1 * X0 * Z1 - X1 * Y1 * Z0 + W1 * X1 * Z0 + W0 * X1 * Y1 - W1 * X1 * Y0;
double G = X0 * Z1 - W0 * Z1 - X1 * Z0 + W1 * Z0 - X0 * Y1 + W0 * Y1 + X1 * Y0 - W1 * Y0;
double H = Y0 * Z1 - X0 * Z1 - Y1 * Z0 + X1 * Z0 + W0 * Y1 - W1 * Y0 - W0 * X1 + W1 * X0;
double I = Y0 * Z1 - W0 * Z1 - Y1 * Z0 + W1 * Z0 + X0 * Y1 - X1 * Y0 + W0 * X1 - W1 * X0;
double detT = A * E * I + B * F * G + C * D * H - A * F * H - B * D * I - C * E * G;
double J = (E * I - F * H) / detT;
double K = (C * H - B * I) / detT;
double L = (B * F - C * E) / detT;
double M = (F * G - D * I) / detT;
double N = (A * I - C * G) / detT;
double O = (C * D - A * F) / detT;
double P = (D * H - E * G) / detT;
double Q = (B * G - A * H) / detT;
double R = (A * E - B * D) / detT;
double a = J * J + M * M + P * P;
double b = J * K + M * N - P * Q;
double c = K * K + N * N - Q * Q;
double d = J * L + M * O - P * R;
double f = K * L + N * O - Q * R;
double g = L * L + O * O - R * R;
double Ex = (c * d - b * f) / (b * b - a * c);
double Ey = (a * f - b * d) / (b * b - a * c);
double Ea = Math.Sqrt(2.0 * (a * f * f + c * d * d + g * b * b - 2.0 * b * d * f - a * c * g) / ((b * b - a * c) * (Math.Sqrt((a - c) * (a - c) + 4.0 * b * b) - (a + c))));
double Eb = Math.Sqrt(2.0 * (a * f * f + c * d * d + g * b * b - 2.0 * b * d * f - a * c * g) / ((a * c - b * b) * (Math.Sqrt((a - c) * (a - c) + 4.0 * b * b) + (a + c))));
double phi = 0;
if (b == 0 && a < c) {
phi = 0;
} else if (b == 0 && a > c) {
phi = Math.PI / 2;
} else if (b != 0 && a < c) {
phi = (Math.PI / 2 - Math.Atan((a - c) / (2 * b))) / 2;
} else if (b != 0 && a > c) {
phi = (Math.PI / 2 - Math.Atan((a - c) / (2 * b))) / 2 + Math.PI / 2;
}
Ellipse el = new Ellipse();
el.Height = Ea * 2;
el.Width = Eb * 2;
el.RenderTransform = new RotateTransform(phi * 180 / Math.PI);
return el;
}
Although four bezier curves should do it quite fine (and is probably the simplest solution), I am proposing a different method here, just for kicks. :-)
Think of your problem this way: Given a regular rectangle, draw an ellipse inside, then deform the rectangle into your final shape.
I don't think your deform transformation is linear, so you probably can't simply find a matrix for it (note: I may be wrong, and would love to be proven wrong; any math buffs here?) Also see edit below.
One method is: draw your ellipse, then pull/push each of the four corners one by one. By deforming only one corner of a shape, you can always interpolate any point on the ellipse curve to its new position by keeping the diagonal between the left and right corners intact.
EDIT: TRANSFORM
Start with a square (and a circle inside).
Notice that all four transformations are either pure linear or affine (i.e. linear + translation), so they are each representable with a transformation matrix. The end result is another affine transformation, which can also be represented by a matrix.
So your circle shape gets transformed by this matrix into the new shape.
I hope I haven't made a mistake in my math...
There's a small bug in Karsten's code around
} else if (b != 0 && a < c) {
phi = (Math.PI / 2 - Math.Atan((a - c) / (2 * b))) / 2;
} else if (b != 0 && a > c) {
It returns phi = 0 when a==c, which is incorrect. Instead, the above lines should be
} else if (b != 0 && a < c) {
phi = (Math.PI / 2 - Math.Atan((a - c) / (2 * b))) / 2;
} else if (b != 0 && a >= c) {
or
} else if (b != 0 && a <= c) {
phi = (Math.PI / 2 - Math.Atan((a - c) / (2 * b))) / 2;
} else if (b != 0 && a > c) {
