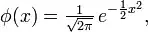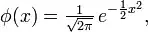Rectangle/Rectangle Collision Detection

Question

I am trying to solve an issue when two rectangles intersect/overlap each other. when this happens, i want to know if intersection is True or False. I found a solution, however it is written in C or C++. I want to write these code in Python.

Here is the source: http://www.jeffreythompson.org/collision-detection/rect-rect.php

Sounds like a simple geometry/maths problem. Once you understand the underlying maths, implenting a solution in *any* programming language should be trivial. — Jesper Juhl, Jan 25 '19 at 17:17

score 2 · Answer 1 · edited Jun 02 '21 at 17:52

This is literally the first line of python code I've ever written (I do know C++ however)

def rectRect(r1x, r1y, r1w, r1h, r2x, r2y, r2w, r2h):

    # are the sides of one rectangle touching the other?

    return r1x + r1w >= r2x and \   # r1 right edge past r2 left
        r1x <= r2x + r2w and \  # r1 left edge past r2 right
        r1y + r1h >= r2y and \   # r1 top edge past r2 bottom
        r1y <= r2y + r2h    # r1 bottom edge past r2 top

IMHO rectRect is a really bad name for the function, I kept it from the linked code however.

score 0 · Answer 2 · answered Oct 22 '21 at 09:59

Following is simple class that can perform both rectangle-rectangle intersection as well as point to rectangle intersection. The difference between earlier solution is that following snippet allows even detection of rotated rectangles.

import numpy as np
import matplotlib.pyplot as plt


class Rectangle:
    def __init__(self, center: np.ndarray, dims: np.ndarray, angle: float):
        self.corners = self.get_rect_points(center, dims, angle)
        self.area = dims[0] * dims[1]

    @staticmethod
    def get_rect_points(center: np.ndarray, dims: np.ndarray, angle: float):
        """
        returns four corners of the rectangle.
        bottom left is the first conrner, from there it goes
        counter clockwise.
        """
        center = np.asarray(center)
        length, breadth = dims
        angle = np.deg2rad(angle)
        corners = np.array([[-length/2, -breadth/2],
                            [length/2, -breadth/2],
                            [length/2, breadth/2],
                            [-length/2, breadth/2]])
        rot = np.array([[np.cos(angle), np.sin(angle)], [-np.sin(angle), np.cos(angle)]])
        corners = rot.dot(corners.T) + center[:, None]
        return corners.T

    def is_point_in_collision(self, p: np.ndarray):
        """
        check if a point is in collision with the rectangle.
        """
        def area_triangle(a, b, c):
            return abs((b[0] * a[1] - a[0] * b[1]) + (c[0] * b[1] - b[0] * c[1]) + (a[0] * c[1] - c[0] * a[1])) / 2

        area = 0
        area += area_triangle(self.corners[0], p, self.corners[3])
        area += area_triangle(self.corners[3], p, self.corners[2])
        area += area_triangle(self.corners[2], p, self.corners[1])
        area += area_triangle(self.corners[1], p, self.corners[0])
        return area > self.area

    def is_intersect(self, rect_2: Rectangle):
        """
        check if any of the four corners of the
        rectangle is in collision
        """
        if not np.all([self.is_point_in_collision(c) for c in rect_2.corners]):
            return True
        return False


def plot_rect(p1, p2, p3, p4, color='r'):
    ax.plot([p1[0], p2[0]], [p1[1], p2[1]], color)
    ax.plot([p2[0], p3[0]], [p2[1], p3[1]], color)
    ax.plot([p3[0], p4[0]], [p3[1], p4[1]], color)
    ax.plot([p4[0], p1[0]], [p4[1], p1[1]], color)
    mid_point = 0.5 * (p1 + p3)
    plt.scatter(mid_point[0], mid_point[1], marker='*')
    plt.xlim([-1, 1])
    plt.ylim([-1, 1])

Following are two samples:

Sample 1:

ax = plt.subplot(111)
st = Rectangle((0.067, 0.476),(0.61, 0.41), 90)
gripper = Rectangle((-0.367, 0.476),(0.21,0.16), 45)
plot_rect(*st.corners)
plot_rect(*gripper.corners)
plt.show()
print(f"gripper and rectangle intersect: {st.is_intersect(gripper)}")

Sample 2:

ax = plt.subplot(111)
st = Rectangle((0.067, 0.476),(0.61, 0.41), 90)
gripper = Rectangle((-0.167, 0.476),(0.21,0.16), 45)
plot_rect(*st.corners)
plot_rect(*gripper.corners)
plt.show()
print(f"gripper and rectangle intersect: {st.is_intersect(gripper)}")

Rectangle/Rectangle Collision Detection

2 Answers2