Let me start the question by providing some boilerplate code we'll use to play around:
mcve_framework.py
import time
from OpenGL.GL import *
from OpenGL.GLU import *
from OpenGL.GLUT import *
import glm
from glm import unProject
from glm import vec2
from glm import vec3
from glm import vec4
# -------- Camera --------
class BaseCamera():
def __init__(
self,
eye=None, target=None, up=None,
fov=None, near=0.1, far=100000
):
self.eye = eye or glm.vec3(0, 0, 1)
self.target = target or glm.vec3(0, 0, 0)
self.up = up or glm.vec3(0, 1, 0)
self.original_up = glm.vec3(self.up)
self.fov = fov or glm.radians(45)
self.near = near
self.far = far
def update(self, aspect):
self.view = glm.lookAt(
self.eye, self.target, self.up
)
self.projection = glm.perspective(
self.fov, aspect, self.near, self.far
)
# def zoom(self, *args):
# delta = -args[1] * 0.1
# self.eye = self.target + (self.eye - self.target) * (delta + 1)
def zoom(self, *args):
x = args[2]
y = args[3]
v = glGetIntegerv(GL_VIEWPORT)
viewport = vec4(float(v[0]), float(v[1]), float(v[2]), float(v[3]))
height = viewport.w
pt_wnd = vec3(x, height - y, 1.0)
pt_world = unProject(pt_wnd, self.view, self.projection, viewport)
ray_cursor = glm.normalize(pt_world - self.eye)
delta = args[1] * 10
self.eye = self.eye + ray_cursor * delta
self.target = self.target + ray_cursor * delta
def load_projection(self):
width = glutGet(GLUT_WINDOW_WIDTH)
height = glutGet(GLUT_WINDOW_HEIGHT)
glMatrixMode(GL_PROJECTION)
glLoadIdentity()
gluPerspective(glm.degrees(self.fov), width / height, self.near, self.far)
def load_modelview(self):
e = self.eye
t = self.target
u = self.up
glMatrixMode(GL_MODELVIEW)
glLoadIdentity()
gluLookAt(e.x, e.y, e.z, t.x, t.y, t.z, u.x, u.y, u.z)
class Camera(BaseCamera):
def rotate_target(self, delta):
right = glm.normalize(glm.cross(self.target - self.eye, self.up))
M = glm.mat4(1)
M = glm.translate(M, self.eye)
M = glm.rotate(M, delta.y, right)
M = glm.rotate(M, delta.x, self.up)
M = glm.translate(M, -self.eye)
self.target = glm.vec3(M * glm.vec4(self.target, 1.0))
def rotate_around_target(self, target, delta):
right = glm.normalize(glm.cross(self.target - self.eye, self.up))
amount = (right * delta.y + self.up * delta.x)
M = glm.mat4(1)
M = glm.rotate(M, amount.z, glm.vec3(0, 0, 1))
M = glm.rotate(M, amount.y, glm.vec3(0, 1, 0))
M = glm.rotate(M, amount.x, glm.vec3(1, 0, 0))
self.eye = glm.vec3(M * glm.vec4(self.eye, 1.0))
self.target = target
self.up = self.original_up
def rotate_around_origin(self, delta):
return self.rotate_around_target(glm.vec3(0), delta)
class GlutController():
FPS = 0
ORBIT = 1
def __init__(self, camera, velocity=100, velocity_wheel=100):
self.velocity = velocity
self.velocity_wheel = velocity_wheel
self.camera = camera
def glut_mouse(self, button, state, x, y):
self.mouse_last_pos = vec2(x, y)
self.mouse_down_pos = vec2(x, y)
if button == GLUT_LEFT_BUTTON:
self.mode = self.FPS
elif button == GLUT_RIGHT_BUTTON:
self.mode = self.ORBIT
def glut_motion(self, x, y):
pos = vec2(x, y)
move = self.mouse_last_pos - pos
self.mouse_last_pos = pos
if self.mode == self.FPS:
self.camera.rotate_target(move * 0.005)
elif self.mode == self.ORBIT:
self.camera.rotate_around_origin(move * 0.005)
def glut_mouse_wheel(self, *args):
self.camera.zoom(*args)
# -------- Miscelanea --------
def render_text(x, y, text):
glColor3f(1, 1, 1)
glRasterPos2f(x, y)
glutBitmapString(GLUT_BITMAP_TIMES_ROMAN_24, text.encode("utf-8"))
def line(p0, p1, color=None):
c = color or glm.vec3(1, 1, 1)
glColor3f(c.x, c.y, c.z)
glVertex3f(p0.x, p0.y, p0.z)
glVertex3f(p1.x, p1.y, p1.z)
def grid(segment_count=10, spacing=1, yup=True):
size = segment_count * spacing
right = glm.vec3(1, 0, 0)
forward = glm.vec3(0, 0, 1) if yup else glm.vec3(0, 1, 0)
x_axis = right * size
z_axis = forward * size
i = -segment_count
glBegin(GL_LINES)
while i <= segment_count:
p0 = -x_axis + forward * i * spacing
p1 = x_axis + forward * i * spacing
line(p0, p1)
p0 = -z_axis + right * i * spacing
p1 = z_axis + right * i * spacing
line(p0, p1)
i += 1
glEnd()
def axis(size=1.0, yup=True):
right = glm.vec3(1, 0, 0)
forward = glm.vec3(0, 0, 1) if yup else glm.vec3(0, 1, 0)
x_axis = right * size
z_axis = forward * size
y_axis = glm.cross(forward, right) * size
glBegin(GL_LINES)
line(x_axis, glm.vec3(0, 0, 0), glm.vec3(1, 0, 0))
line(y_axis, glm.vec3(0, 0, 0), glm.vec3(0, 1, 0))
line(z_axis, glm.vec3(0, 0, 0), glm.vec3(0, 0, 1))
glEnd()
# -------- Mcve --------
class BaseWindow:
def __init__(self, w, h):
self.width = w
self.height = h
glutInit()
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH)
glutInitWindowSize(w, h)
glutCreateWindow('OpenGL Window')
self._startup()
glutReshapeFunc(self.reshape)
glutDisplayFunc(self._display)
glutMouseFunc(self.controller.glut_mouse)
glutMotionFunc(self.controller.glut_motion)
glutMouseWheelFunc(self.controller.glut_mouse_wheel)
glutKeyboardFunc(self.keyboard_func)
glutIdleFunc(self.idle_func)
def keyboard_func(self, *args):
try:
key = args[0].decode("utf8")
if key == "\x1b":
glutLeaveMainLoop()
if key in ['1']:
if key == '1':
self.index_camera = "BPL"
self.camera = self.cameras[self.index_camera]
self.controller.camera = self.camera
except Exception as e:
import traceback
traceback.print_exc()
def display(self):
pass
def startup(self):
pass
def _startup(self):
glEnable(GL_DEPTH_TEST)
params = {
"eye": glm.vec3(0, 150, 150),
"target": glm.vec3(0, 0, 0),
"up": glm.vec3(0, 1, 0)
}
self.start_time = time.time()
self.cameras = {
"BPL": Camera(**params)
}
self.index_camera = "BPL"
self.yup = True
self.camera = self.cameras[self.index_camera]
self.model = glm.mat4(1)
self.controller = GlutController(self.camera)
glPolygonMode(GL_FRONT_AND_BACK, GL_LINE)
self.startup()
def run(self):
glutMainLoop()
def idle_func(self):
glutPostRedisplay()
def reshape(self, w, h):
glViewport(0, 0, w, h)
self.width = w
self.height = h
def render_points(self, vertices):
glColor3f(0.0, 0.0, 0.0)
glBegin(GL_POINTS)
for v in vertices:
glVertex3f(v.x, v.y, v.z)
glEnd()
def render_triangles(self, vertices):
glBegin(GL_TRIANGLES)
for i in range(0, len(vertices), 3):
v0 = vertices[i]
v1 = vertices[i + 1]
v2 = vertices[i + 2]
glVertex3f(v0.x, v0.y, v0.z)
glVertex3f(v1.x, v1.y, v1.z)
glVertex3f(v2.x, v2.y, v2.z)
glEnd()
def render_quads(self, vertices):
glBegin(GL_QUADS)
for i in range(0, len(vertices), 4):
v0 = vertices[i]
v1 = vertices[i + 1]
v2 = vertices[i + 2]
v3 = vertices[i + 3]
glVertex3f(v0.x, v0.y, v0.z)
glVertex3f(v1.x, v1.y, v1.z)
glVertex3f(v2.x, v2.y, v2.z)
glVertex3f(v3.x, v3.y, v3.z)
glEnd()
def render_indexed_triangles(self, indices, vertices):
glBegin(GL_TRIANGLES)
for i in indices:
for j in range(3):
v = vertices[i[j]]
glVertex3f(v.x, v.y, v.z)
glEnd()
def render_indexed_quads(self, indices, vertices):
glBegin(GL_QUADS)
for f1, f2 in zip(indices[::2], indices[1::2]):
i = [f1[0], f1[1], f1[2], f2[2]]
for j in range(4):
v = vertices[i[j]]
glVertex3f(v.x, v.y, v.z)
glEnd()
def _display(self):
self.camera.update(self.width / self.height)
glClearColor(0.2, 0.3, 0.3, 1.0)
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)
self.camera.load_projection()
self.camera.load_modelview()
self.display()
glLineWidth(5)
axis(size=70, yup=True)
glLineWidth(1)
grid(segment_count=7, spacing=10, yup=True)
glMatrixMode(GL_PROJECTION)
glLoadIdentity()
glOrtho(-1, 1, -1, 1, -1, 1)
glMatrixMode(GL_MODELVIEW)
glLoadIdentity()
info = "\n".join([
"{}: Camera - {}".format(i, k) for i, k in enumerate(self.cameras.keys())
])
render_text(-1.0, 1.0 - 0.1, info)
render_text(-1.0, -1.0, "{} camera is active".format(self.index_camera))
glutSwapBuffers()
In case you want to use the above code you'll just need to install pyopengl and pygml. After that, you can just create your own BaseWindow subclass, override startup and render and you should have a very basic glut window with simple functionality such as camera rotation/zooming as well as some methods to render points/triangles/quads and indexed_triangles/indexed_quads.
QUESTION
And now the real question, consider this little snippet:
mcve_torusknot.py
from math import cos
from math import pi
from math import sin
from OpenGL.GL import *
from OpenGL.GLU import *
from OpenGL.GLUT import *
from glm import cross
from glm import normalize
from glm import vec3
from mcve_framework import BaseWindow
def sample(theta, p, q, out):
r = cos(q * theta) + 2.0
out.x = r * cos(p * theta)
out.y = r * sin(q * theta)
out.z = -sin(q * theta)
def gen_torusknot(tess_u, tess_v, p, q):
vertices = []
pp = vec3()
centerpoint = vec3()
nextpoint = vec3()
T = vec3()
B = vec3()
N = vec3()
r2 = 5.0
for u in range(tess_u):
theta = (u / tess_u) * 2 * pi
sample(theta, p, q, centerpoint)
theta = (u + 1) * 2 * pi / tess_u
sample(theta, p, q, nextpoint)
T = (nextpoint - centerpoint)
N = (nextpoint + centerpoint)
B = normalize(cross(T, N))
N = normalize(cross(B, T))
for v in range(tess_v):
theta = (v / tess_v) * 2 * pi
pointx = sin(theta) * r2
pointy = cos(theta) * r2
pp = N * pointx + B * pointy + centerpoint
vertices.append(pp * 10)
return vertices
class McveTorusKnot(BaseWindow):
def __init__(self, *args, **kwargs):
super().__init__(*args, **kwargs)
def startup(self):
self.torusknot = gen_torusknot(60, 60, 1.000000001, 0.000000001)
def display(self):
glPointSize(3)
glPushMatrix()
self.render_points(self.torusknot)
glPopMatrix()
if __name__ == '__main__':
window = McveTorusKnot(800, 600)
window.run()
The end goal here is to figure out how to generate and render a torus knots. But before such an ambitious goal I'd like to figure out why when using p=1 and q=0 parameters I'm not getting a simple torus like the one shown here https://www.geeks3d.com/20140516/pq-torus-knot/, instead I'm get something like this:
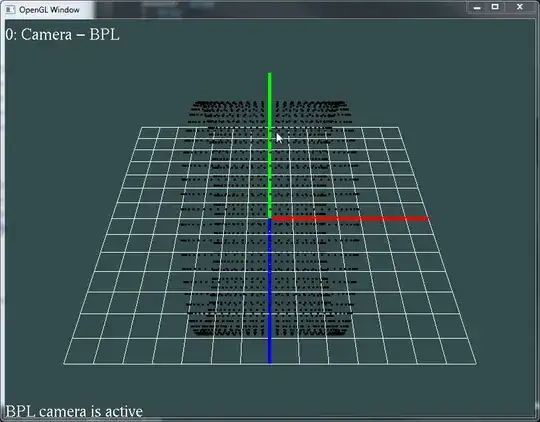
So yeah, that's basically my question, first of all, I'd like to know what's wrong in my above code so I'm not getting a simple torus from the general formula and after that... I'd like to know what's the way to create the mesh connectivity (aka indices, no matter triangles/quads/triangle strips)?
Note: For the sake of simplicity at this point normals or texture coordinates are irrelevant, just to know how to generate the position vertices/indices of the mesh properly will be more than good enough :)