Opacity in EPS figures

Question

When saving graphics in Mathematica, is it possible to save figures with opacity in EPS format? For example,

Plot[Evaluate[Table[BesselJ[n, x], {n, 4}]], {x, 0, 10}, 
 Filling -> Axis]

gives the following figure which saves neatly in any format other than EPS.

If I try saving to EPS (in Mathematica 7), the result looks like

In Mathematica 8 it looks like

Does anyone know how to get opacity in EPS plots (or if that is even possible)? The 'use rasterization for transparency' option doesn't look as impressive as a true EPS on zooming.

Answer 1

I usually Rasterize my graphics in this situation. Try

Rasterize[Plot[Evaluate[Table[BesselJ[n, x], {n, 4}]],
  {x, 0, 10}, Filling -> Axis], RasterSize -> 600, ImageSize -> 400]

Of course, the result will not be scalable and can take up more memory. You can partially solve the scalability problem by setting the RasterSize larger than the ImageSize, as I have done here.

Answer 2

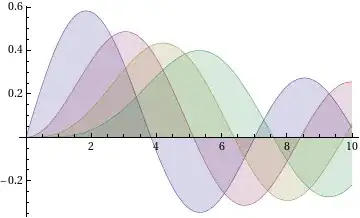
OK, so EPS can not support true transparency/opacity - but that doesn't mean that Mathematica 7 is excused for doing such a bad job. As evidenced my Mathematica 8, it is possible to make it look better.

The problem with Mathematica 7's output is that it uses the same color for the fill as for the curves, when you really want a lighter color. EPS is a plain text format, so it's quite easy to write a quick hack. Here's a quick tute on PS graphics.

In PS graphics, you define a path then you say whether you want it stroked (lines) or filled (areas) - or other things we don't need to worry about. Colors are set and stay there until they are reset. So I simply import the EPS produced by Mma7 and find all filled paths. For each filled path you find the previous color and reset the color just above the fill command to be something lighter.

So here's an example (I haven't bothered packaging it up into a single script/module). All output is from Mathematica 7.0.1

p = Plot[Evaluate[Table[BesselJ[n, x], {n, 4}]], {x, 0, 10}, Filling -> Axis]

Export to an EPS file using Export["BesselJs7.eps", p]. This produces a horrible graphic like

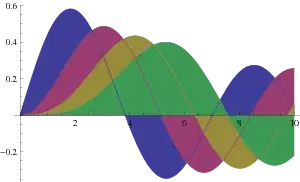
OK, now the "fix"

pList = Import["BesselJs7.eps", "List"];  (* Import image as a list of strings *)
FList = Flatten@Position[pList, "F"];     (* find all fill commands            *)

Note that the EPS file has the line /F { fill} bind def that defines the shortcut F. Also, you can check that pList[[FList - 1]] yields a list of "closepath"s.

FColorList = {}; (* get list of colors associated with fills *)
Catch[Do[
  i = 0; rgb = True; newpath = True;
  While[rgb || newpath,
   (*Print[{f,i,f-i,rgb,newpath,pList[[f-i]]}];*)
   If[rgb && StringMatchQ[pList[[f - i]], __ ~~ "r"], rgb = False; 
    AppendTo[FColorList, pList[[f - i]]]];
   If[newpath && StringMatchQ[pList[[f - i]], "newpath" ~~ __], 
    newpath = False; np[f] = f - i];
   If[f - i == 1, Throw[{f, rgb, newpath}]];
   i++],
  {f, FList}]]

Now a hack to create the new colors - all I do is add .5 to each rgb value. This can definitely be made better:

FColorListNew = Table[Most@ToExpression@StringSplit[f] + .5, 
                {f, FColorList}] /. _?(# > 1 &) -> 1.;
FColorListNew = Table[StringJoin[{Riffle[ToString /@ f, " "], " r"}],
                {f, FColorListNew}];

Finally, insert the new colors and write it back out:

Do[pList = Insert[pList, FColorListNew[[i]], np[FList[[i]]] + i], 
   {i, Length[FList]}]
Export["BesselJsFixed.eps", pList, "List"]

Some things, like finding the newpath locations, are unnecessary and the whole thing can probably be tidied up. But I've spent enough time on it for now!

Answer 3

Building on Mark's answer, to export a PNG with transparency, use:

Export[
  "testfile.png",
  Plot[Evaluate[Table[BesselJ[n, x], {n, 4}]], {x, 0, 10}, Filling -> Axis],
  ImageSize -> 600,
  Background -> None
]