How to broadcast or vectorize a linear interpolation of a 2D array that uses scipy.ndimage map_coordinates?

Question

I have recently hit a roadblock when it comes to performance. I know how to manually loop and do the interpolation from the origin cell to all the other cells by brute-forcing/looping each row and column in 2d array.

however when I process a 2D array of a shape say (3000, 3000), the linear spacing and the interpolation come to a standstill and severely hurt performance.

I am looking for a way I can optimize this loop, I am aware of vectorization and broadcasting just not sure how I can apply it in this situation.

I will explain it with code and figures

import numpy as np
from scipy.ndimage import map_coordinates
m = np.array([
    [10,10,10,10,10,10],
    [9,9,9,10,9,9],
    [9,8,9,10,8,9],
    [9,7,8,0,8,9],
    [8,7,7,8,8,9],
    [5,6,7,7,6,7]])

origin_row = 3
origin_col = 3
m_max = np.zeros(m.shape)
m_dist = np.zeros(m.shape)

rows, cols = m.shape
for col in range(cols):
    for row in range(rows):
        # Get spacing linear interpolation
        x_plot = np.linspace(col, origin_col, 5)
        y_plot = np.linspace(row, origin_row, 5)

        # grab the interpolated line
        interpolated_line = map_coordinates(m,
                                      np.vstack((y_plot,
                                                 x_plot)),
                                      order=1, mode='nearest')
        m_max[row][col] = max(interpolated_line)
        m_dist[row][col] = np.argmax(interpolated_line)

print(m)
print(m_max)
print(m_dist)

As you can see this is very brute force, and I have managed to broadcast all the code around this part but stuck on this part. here is an illustration of what I am trying to achieve, I will go through the first iteration

1.) the input array

2.) the first loop from 0,0 to origin (3,3)

3.) this will return [10 9 9 8 0] and the max will be 10 and the index will be 0

5.) here is the output for the sample array I used

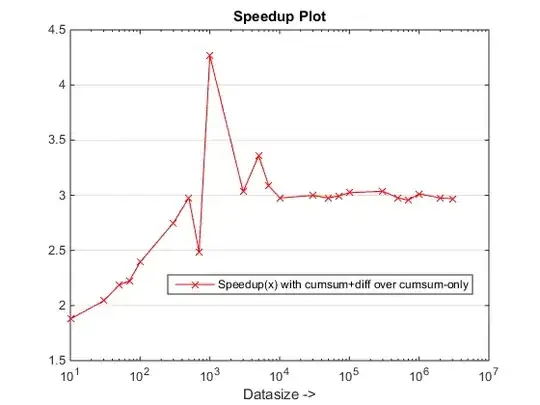
Here is an update of the performance based on the accepted answer.

Answer 1

To speed up the code, you could first create the x_plot and y_plot outside of the loops instead of creating them several times each one:

#this would be outside of the loops
num = 5
lin_col = np.array([np.linspace(i, origin_col, num) for i in range(cols)])
lin_row = np.array([np.linspace(i, origin_row, num) for i in range(rows)])

then you could access them in each loop by x_plot = lin_col[col] and y_plot = lin_row[row]

Second, you can avoid both loops by using map_coordinates on more than just one v_stack for each couple (row, col). To do so, you can create all the combinaisons of x_plot and y_plot by using np.tile and np.ravel such as:

arr_vs = np.vstack(( np.tile( lin_row, cols).ravel(),
                     np.tile( lin_col.ravel(), rows)))

Note that ravel is not used at the same place each time to get all the combinaisons. Now you can use map_coordinates with this arr_vs and reshape the result with the number of rows, cols and num to get each interpolated_line in the last axis of a 3D-array:

arr_map = map_coordinates(m, arr_vs, order=1, mode='nearest').reshape(rows,cols,num)

Finally, you can use np.max and np.argmax on the last axis of arr_map to get the results m_max and m_dist. So all the code would be:

import numpy as np
from scipy.ndimage import map_coordinates
m = np.array([
    [10,10,10,10,10,10],
    [9,9,9,10,9,9],
    [9,8,9,10,8,9],
    [9,7,8,0,8,9],
    [8,7,7,8,8,9],
    [5,6,7,7,6,7]])

origin_row = 3
origin_col = 3
rows, cols = m.shape

num = 5
lin_col = np.array([np.linspace(i, origin_col, num) for i in range(cols)])
lin_row = np.array([np.linspace(i, origin_row, num) for i in range(rows)])

arr_vs = np.vstack(( np.tile( lin_row, cols).ravel(),
                     np.tile( lin_col.ravel(), rows)))

arr_map = map_coordinates(m, arr_vs, order=1, mode='nearest').reshape(rows,cols,num)
m_max = np.max( arr_map, axis=-1)
m_dist = np.argmax( arr_map, axis=-1)

print (m_max)
print (m_dist)

and you get like expected:

#m_max
array([[10, 10, 10, 10, 10, 10],
       [ 9,  9, 10, 10,  9,  9],
       [ 9,  9,  9, 10,  8,  9],
       [ 9,  8,  8,  0,  8,  9],
       [ 8,  8,  7,  8,  8,  9],
       [ 7,  7,  8,  8,  8,  8]])
#m_dist
array([[0, 0, 0, 0, 0, 0],
       [0, 0, 2, 0, 0, 0],
       [0, 2, 0, 0, 0, 0],
       [0, 1, 0, 0, 0, 0],
       [0, 2, 0, 0, 0, 0],
       [1, 1, 2, 1, 2, 1]])

EDIT: lin_col and lin_row are related, so you can do faster:

if cols >= rows:
    arr = np.arange(cols)[:,None]
    lin_col = arr + (origin_col-arr)/(num-1.)*np.arange(num)
    lin_row = lin_col[:rows] + np.linspace(0, origin_row - origin_col, num)[None,:]
else:
    arr = np.arange(rows)[:,None]
    lin_row = arr + (origin_row-arr)/(num-1.)*np.arange(num)
    lin_col = lin_row[:cols] + np.linspace(0, origin_col - origin_row, num)[None,:]

Answer 2

Here is a sort-of-vectorized approach. It is not very optimized and there may be one or two index-off-by-one errors, but it may give you ideas.

Two examples a monochrome 384x512 test pattern and a "real" 3-channel 768x1024 image. Both are uint8. This takes half a minute on my machine.

For larger images one would require more RAM than I have (8GB). Or one would have to break it down into smaller chunks.

And the code

import numpy as np

def rays(img, ctr):
    M, N, *d = img.shape
    aidx = 2*(slice(None),) + (img.ndim-2)*(None,)
    m, n = ctr
    out = np.empty_like(img)
    offsI = np.empty(img.shape, np.uint16)
    offsJ = np.empty(img.shape, np.uint16)
    img4, out4, I4, J4 = ((x[m:, n:], x[m:, n::-1], x[m::-1, n:], x[m::-1, n::-1]) for x in (img, out, offsI, offsJ))
    for i, o, y, x in zip(img4, out4, I4, J4):
        for _ in range(2):
            M, N, *d = i.shape
            widths = np.arange(1, M+1, dtype=np.uint16).clip(None, N)
            I = np.arange(M, dtype=np.uint16).repeat(widths)
            J = np.ones_like(I)
            J[0] = 0
            J[widths[:-1].cumsum()] -= widths[:-1]
            J = J.cumsum(dtype=np.uint16)
            ii = np.arange(1, 2*M-1, dtype=np.uint16) // 2
            II = ii.clip(None, I[:, None])
            jj = np.arange(2*M-2, dtype=np.uint32) // 2 * 2 + 1
            jj[0] = 0
            JJ = ((1 + jj) * J[:, None] // (2*(I+1))[:, None]).astype(np.uint16).clip(None, J[:, None])
            idx = i[II, JJ].argmax(axis=1)
            II, JJ = (np.take_along_axis(ZZ[aidx] , idx[:, None], 1)[:, 0] for ZZ in (II, JJ))
            y[I, J], x[I, J] = II, JJ
            SH = II, JJ, *np.ogrid[tuple(map(slice, img.shape))][2:]
            o[I, J] = i[SH]
            i, o = i.swapaxes(0, 1), o.swapaxes(0, 1)
            y, x = x.swapaxes(0, 1), y.swapaxes(0, 1)
    return out, offsI, offsJ

from scipy.misc import face

f = face()
fr, *fidx = rays(f, (200, 400))
s = np.uint8((np.arange(384)[:, None] % 41 < 2)&(np.arange(512) % 41 < 2))
s = 255*s + 128*s[::-1, ::-1] + 64*s[::-1] + 32*s[:, ::-1]
sr, *sidx = rays(s, (200, 400))

import Image
Image.fromarray(f).show()
Image.fromarray(fr).show()
Image.fromarray(s).show()
Image.fromarray(sr).show()