Recently, I was looking for a faster alternative to the math exp(x) function. I found something that suited me very well, most often this solution is called Ankerl algorithm. Refs :
https://github.com/ekmett/approximate/blob/master/cbits/fast.c https://martin.ankerl.com/2012/01/25/optimized-approximative-pow-in-c-and-cpp/
There is typical Ankerl exp function implementation on C
double exp_fast(double a)
{
union { double d; long long x; } u;
u.x = (long long)(6497320848556798LL * a + 0x3fef127e83d16f12LL);
return u.d;
}
int main()
{
for (float x = 0; x < 10; x += 0.01)
std::cout << x << '\t'
<< exp(x) << '\t'
<< exp_fast(x)
<< std::endl;
return 0;
}
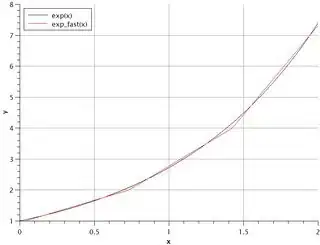
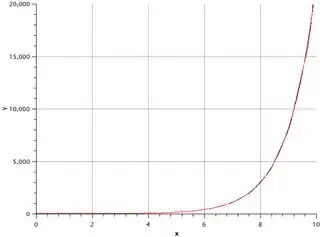
Unfortunately I could not find a description of this algorithm. Perhaps in the literature it is called something else. I tried to plot this function and was very surprised - this is a piecewise linear approximation of the exponent function! It works perfectly in a very wide range of output values. All graphs contain about a thousand points (click to zoom)
I could not understand exactly how it works despite all efforts. It surprises me how such a simple code can give such good approximation. I will be very grateful if someone can clearly explain how this works and from what considerations the values 6497320848556798LL, 0x3fef127e83d16f12LL are chosen. And the second thing - is it safe to use such a solution or is it a sort of dirty hack which should be avoided?