How to represent density information on a matplotlib 3-D scatter plot

Question

I am trying to plot the r,g,b channels in an image as a 3-D scatter plot.

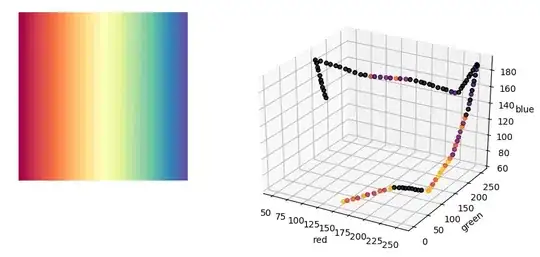
This works well when i have a black and white image as i get a scatter plot with just two distinct clusters at two ends of the scatter plot.

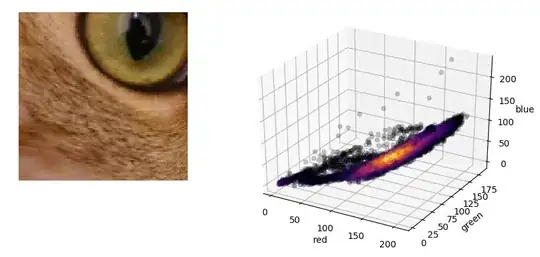
However for color images the scatter plot does not make much sense visually because there are r,g,b values corresponding to many points in the color space in the image.

So i end up with something like the image shown below -

What i would like to achieve is somehow represent density information. For example if the number of points corresponding to (255,255,255) are 1000 and the number of points corresponding to (0,0,0) are only 500 then i want (255,255,255) to be dark red and (0,0,0) to be yellow/orangish

How do i achieve this in matplotlib? I am okay with some sort of bubble effect as well where the (255,255,255) is represented as a bigger bubble compared to (0,0,0) although i feel density information encoded as color information would be more visually appealing

Answer 1

Here's an attempt using Gaussian KDE. It's still far from perfect and the result largely depends on the estimation parameters (bw_method). There is perhaps a simpler way, maybe something using np.unique to get the frequency of each unique colour.

The idea is to estimate color density distribution as a multivariate gaussian mixture and use that as a colormap for the scatter plot.

It's a bit slow for anything serious but I think it gives nice results with small enough images. Maybe some FFT+convolution based estimation method could be faster.

Let's see some code. Nothing fancy: it flattens and reshapes image data the way gaussian_kde likes it and return RGB and density components. You can play with bw_method and see how the results change, the bigger, the smoother density you'll get.

from scipy.stats import gaussian_kde

def img_to_rgbk(img, bw=0.1):
    rgb = img.reshape(-1, 3).T
    k = gaussian_kde(rgb, bw_method=bw)(rgb)
    r, g, b = rgb

    return r, g, b, k

Here's the results with a toy image

img = chelsea()[100:200, 100:200]

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

r, g, b, k = img_to_rgbk(img, bw=0.5)
ax.scatter(r, g, b, c=k, alpha=0.2)

Notice c=k is used to set map marker color to the density information, alpha is needed to see a bit through the cloud.

Chelsea

Random colors

Gradient

Note here you can see how the wrong choice of bandwidth can be misleading. A small enough bw_method should reveal essentially a single color per column, repeated along rows. So every dot should have the same color (and it will with the right bandwidth).

Gradient + noise

Here with a better bandwidth and some noise to spread the colors. Notice the bigger density around the white-ish area where the discontinuity in the no-noise plot becomes a density maximum.