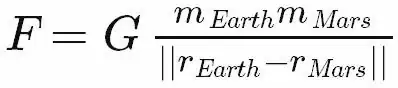Am i miss-using numpy random number generator for bootstrapping?

Question

I attempted to write some code to create a bootstrap distribution and, although it compiles, I'm not sure it is working correctly. Some background: A student at the school where I teach has been systematically finding the combination to the locks on the laptops in our computer lab to screw with our computer teacher (who is, fortunately, not me). Each lock has three entries with the numbers 0-9. I calculate that there are 10^3 possible combinations per lock. He kept detailed lists of combinations he has already tried for each lock so each successive attempt samples one combination without replacement. I am trying to simulate this to get an idea of how many attempts he made to unlock all of these computers (there are 12 computers in lab) by finding an expected value for the number of times it would take to unlock one. This sounds like a hypergeometric distribution to me. The code I wrote is:

import numpy as np

def lock_hg(N):

    final_counts = []
    for i in range(N):
        count = 1
        combs = list(np.arange(1,1001,1))
        guess = np.random.randint(1,1000)
        for k in range(1000):
            a = np.random.choice(combs, 1)
            if a == guess:
                final_counts.append(count)
                break
            else:
                count = count + 1
                combs.remove(a)

    return(final_counts)

The histogram plt.hist(final_counts) when lock_hg(1000) is called looks fairly uniform with 40 or 50 attempts being just as common as 900 or 950. I thought it would look more like a normal distribution centered at 500. I'm not sure if there is a problem with the code or I am just misunderstanding the math. Is this code appropriate for the problem? If not, how can I fix it? If it is working, is there a more efficient way to do this and, if so, what is it?

Answer 1

Imagine generating a grid of combinations, with each row representing a lock and each column value a possible combination for that lock. For example, suppose there are 10 locks and only 5 possible combinations per lock. You can generate them all in a random order like this:

In [42]: np.random.seed(2018) # to make the example reproducible
In [43]: grid = np.random.random((10,5)).argsort(axis=1); grid
Out[43]: 
array([[1, 3, 4, 0, 2],
       [4, 0, 2, 3, 1],
       [3, 4, 2, 0, 1],
       [2, 1, 3, 4, 0],
       [1, 3, 0, 4, 2],
       [1, 0, 4, 3, 2],
       [2, 0, 1, 3, 4],
       [2, 0, 3, 4, 1],
       [2, 3, 1, 0, 4],
       [2, 4, 0, 3, 1]])

Next, let's pick a random combination for each of the 10 locks:

In [48]: combo = np.random.choice(5, size=10, replace=True); combo
Out[48]: array([3, 2, 3, 3, 4, 4, 4, 3, 2, 3])

We can think of grid as indicating the order in which combinations are tried for each lock. And we can take combo to be the actual combination for each lock.

We can also visualize the location of the matches using:

plt.imshow((grid == combo[:, None])[::-1], origin='upper')

and we can find the location of each successful match in our grid by using argmax:

In [73]: (grid == combo[:, None]).argmax(axis=1)
Out[73]: array([1, 2, 0, 2, 3, 2, 4, 2, 0, 3])

argmax returns the index (location) of a match for each row. These index numbers also indicate the number of attempts required to find each match. Well, almost. Since Python is 0-index based, argmax will return 0 if the match occurs on the first attempt. So we need to add 1 to (grid == combo[:, None]).argmax(axis=1) to obtain the true number of attempts.

So, we are looking for the distribution of (grid == combo[:, None]).argmax(axis=1) + 1. Now that we've worked out the computation for 10 locks and 5 combinations, it is easy to increase this to, say, 10000 locks and 1000 combinations:

import numpy as np
import matplotlib.pyplot as plt
np.random.seed(2018)

num_locks = 10000
num_combos = 1000

grid = np.random.random((num_locks, num_combos)).argsort(axis=1)
combo = np.random.choice(num_combos, size=num_locks, replace=True)
attempts = (grid == combo[:, None]).argmax(axis=1) + 1

plt.hist(attempts, density=True)
plt.show()

This method of picking a random location in the grid makes it clear that the distribution should be uniform -- it's just as likely that the right combo occurs at the beginning, as at the end, or at any location in between.

Answer 2

A uniform distribution is expected, yes. The code is fine.

A possible optimization would be to swap the chosen key with the last one in the list, before removing it. This would avoid touching all the ones in between.

Answer 3

Two improvements you can make:

1. Python has a built-in random number generator. https://docs.python.org/2/library/random.html

import random

for i in range(5):
    print(random.randint(0, 100))

10
38
53
83
23

2. If you're trying to iterate through all possible combinations to get into something (like a lock), it's better to go up by one instead of using a random number generator. I could be misunderstanding the question a bit as I'm not sure whether you're trying to figure out how he did it.