Wrong Voigt output/convolution with asymmetric x input

Question

At the moment I am fitting a Gaussian or Lorentz to my data but both don't fit well enough and I want to switch to Voigt fitting, a convolution of them both.

I retrieved the Voigt function from https://www.originlab.com/doc/Origin-Help/Voigt-FitFunc and wrote it into python.

import numpy as np
import matplotlib.pyplot as plt

def lorentz_voigt(x, A, xc, wL):
    return (2*A / np.pi) * (wL / ((4*(x.astype(float) - xc)**2) + wL**2))

def gauss_voigt(x, wG):
    return np.sqrt((4*np.log(2)) / np.pi) * ((np.exp(-(((4*np.log(2)) / (wG**2))*(x.astype(float))**2))) / (wG))

def Voigt(x, xc, A, wG, wL):
    return np.convolve(lorentz_voigt(x, A, xc, wL), gauss_voigt(x, wG), 'same')

symx = np.linspace(-100, 100, 1001)
asymx = np.linspace(0, 100, 1001)
symy = Voigt(symx, 50, 1, 5, 5)
asymy = Voigt(asymx, 50, 1, 5, 5)
plt.clf()
plt.plot(symx, symy)
plt.plot(asymx, asymy)

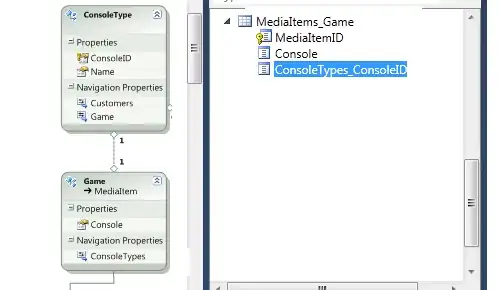
As seen in the plot below the Voigt function with an asymmetric x-axis input, in orange, does not reproduce the correct Voigt profile as seen in blue.

My data is in wavenumbers from 600-4000 cm^-1 and I would like to know if I would have to add zeros to my data from -4000 to 600 cm^-1 because this is a pure mathematical limitation of convolution or is there a mistake in/solution for my code?

@JamesPhillips The data seen in the plot is created in the script above. The actual data from the experiment is irrelevant at this stage of troubleshooting. The Voigt function is passed to curve_fit, however the function does not recreate the correct profile thus fitting fails. — Terranees, Nov 06 '18 at 07:56
There is another way to calculate voigt lineshapes which does not involve convolution: `V(x,sig,gam) = Re(w(z))/(sig*sqrt(2*pi))` where `z = (x+i*gam)/(sig*sqrt(2))` and `Re(w(z))` is the real part of the Faddeeva function. The latter is in scipy as `scipy.special.wofz`. — Christian K., Nov 06 '18 at 13:01
The default initial parameters used by curve_fit are all 1.0 by default, and this is not optimal in all cases. Scipy's optimize.differential_evolution genetic algorithm can be used to determine initial parameter estimates, and I had hoped to give an example of this using your experimental data, hence my request for the link to same. — James Phillips, Nov 06 '18 at 16:53
@Terranees It looks like you are working with raman spectra and do not want to use Origin. Have a look at [peak-o-mat](http://lorentz.sf.net). It is written in python. — Christian K., Nov 07 '18 at 20:57
@Christian K. peak-o-mat moved. It is now at http://qceha.net/ — Christian K., May 04 '21 at 20:38

Christian K. · Accepted Answer · 2018-11-07T20:48:30.737

The convolution does not know anything about the x axis. Best have it return the full convolution and than shrink that to the original x-range, e.g.:

import numpy as np
import matplotlib.pyplot as plt

def lorentz_voigt(x, A, xc, wL):
    return (2*A / np.pi) * (wL / ((4*(x.astype(float) - xc)**2) + wL**2))

def gauss_voigt(x, xc, wG):
    return np.sqrt((4*np.log(2)) / np.pi) * ((np.exp(-(((4*np.log(2)) / (wG**2))*((x-xc).astype(float))**2))) / (wG))

def Voigt(x, xc, A, wG, wL):
    return np.convolve(lorentz_voigt(x, A, xc, wL), gauss_voigt(x, xc, wG), 'full')

symx = np.linspace(-100, 100, 1001)
asymx = np.linspace(0, 200, 1001)
symy = Voigt(symx, 50, 1, 5, 5)[::2]
asymy = Voigt(asymx, 50, 1, 5, 5)[::2]

plt.clf()
plt.plot(symx, symy,'r')
plt.plot(asymx, asymy,'b--')

Also note that your definition of gauss_voigt misses the center corrdinate xc.

As I said in the comment above there is another way to calculate the voigt function which is not based on convolution. Convolution is expensive in terms of computation time which can get annoying when used as fit model. The following sample code does not need convolution.

import matplotlib.pyplot as plt
import numpy as np
from scipy.special import wofz

def voigt(x, amp, pos, fwhm, shape):
    tmp = 1/wofz(np.zeros((len(x))) +1j*np.sqrt(np.log(2.0))*shape).real
    return tmp*amp*wofz(2*np.sqrt(np.log(2.0))*(x-pos)/fwhm+1j*np.sqrt(np.log(2.0))*shape).real

x = np.linspace(0, 100, 1001)
y0 = voigt(x, 1, 50, 5, 0)
y1 = voigt(x, 1, 50, 5, 1)
plt.plot(x,y0,'k',label='shape = 0')
plt.plot(x,y1,'b',label='shape = 1')
plt.legend(loc=0)
plt.show()

I was under the impression that the 'same' mode would do the same, but apparently not. I did noticed that the xc was missing in the Gaussian component of the function given on https://www.originlab.com/doc/Origin-Help/Voigt-FitFunc. I assumed this was because the Gauss was normalized for the convolution, or something similar. Do you have a justification for adding xc to gauss_voigt? — Terranees, Nov 07 '18 at 12:06

Wrong Voigt output/convolution with asymmetric x input

1 Answers1