Eliminate a variable to relate two functions in Python using SymPy

Question

I have two equations that are parametrized by a variable "t". These look like:

X = p(t) 
Y = q(t)

where p and q are polynomials in t. I want to use Python's SymPy library to eliminate the t variable and express Y = F(X) for some function X. I have tried using solve() in SymPy but this is not working too well. I know that Maple and Mathematica both have eliminate() functions that can accomplish this, but I wanted to know if Python might have a general function that does this.

I can duplicate the example provided in the Mathematica documentation using Sympy, albeit somewhat inelegantly using solve. If you want details please let me know. — Bill Bell, Oct 31 '18 at 23:19
Hi Bill, yes certainly! Will you be able to comment or write it as an answer? Thanks. — Kshitij Kulkarni, Oct 31 '18 at 23:31
What about solving the first equation for *t*, plugging it into *Y* and then simplifying it? (There may very well be a better solution; I'm not very familiar with sympy) — user8408080, Nov 01 '18 at 00:51

score 3 · Answer 1 · answered Nov 01 '18 at 03:34

I refer to this example from the 'Scope' section of https://reference.wolfram.com/language/ref/Eliminate.html.

Eliminate[2 x + 3 y + 4 z == 1 && 9 x + 8 y + 7 z == 2, z]

>>> from sympy import *
>>> var('x y z')
(x, y, z)
>>> solve(2*x+3*y+4*z-1, z)
[-x/2 - 3*y/4 + 1/4]
>>> solve(9*x+8*y+7*z-2, z)
[-9*x/7 - 8*y/7 + 2/7]
>>> (-9*x/7 - 8*y/7 + Rational(2,7))-(-x/2 - 3*y/4 + Rational(1,4)).simplify()
-11*x/14 - 11*y/28 + 1/28
>>> 28*((-9*x/7 - 8*y/7 + Rational(2,7))-(-x/2 - 3*y/4 + Rational(1,4)).simplify())
-22*x - 11*y + 1

Solve each equation for z.
Subtract one expression for z from the other.
Note only that numeric fractions need to be coded — I've used Rational because I forget other methods — so that fractional arithmetic is used.
I multiply through to get rid of the denominators.
This approach will work only for the elimination of a single variable. I haven't considered the second and subsequent examples.

I hope this is useful.

score 3 · Answer 2 · answered Nov 06 '18 at 17:36

Here is a lightly tested simple routine

def eliminate(eqs, z):
    """return eqs with parameter z eliminated from each equation; the first
    element in the returned list will be the definition of z that was used
    to eliminate z from the other equations.

    Examples
    ========

    >>> eqs = [Eq(2*x + 3*y + 4*z, 1),
    ...        Eq(9*x + 8*y + 7*z, 2)]
    >>> eliminate(eqs, z)
    [Eq(z, -x/2 - 3*y/4 + 1/4), Eq(11*x/2 + 11*y/4 + 7/4, 2)]
    >>> Eq(y,solve(_[1], y)[0])
    Eq(y, -2*x + 1/11)
    """
    from sympy.solvers.solveset import linsolve
    Z = Dummy()
    rv = []
    for i, e in enumerate(eqs):
        if z not in e.free_symbols:
            continue
        e = e.subs(z, Z)
        if z in e.free_symbols:
            break
        try:
            s = linsolve([e], Z)
            if s:
                zi = list(s)[0][0]
                rv.append(Eq(z, zi))
                rv.extend([eqs[j].subs(z, zi)
                    for j in range(len(eqs)) if j != i])
                return rv
        except ValueError:
            continue
    raise ValueError('only a linear parameter can be eliminated')

There is a more complex routine at this issue.

score 1 · Answer 3 · answered Dec 25 '19 at 18:22

Suppose you wanted to solve the equations

eqs

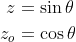
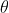for z_o as a function of . This can be done by solving for both z_o and theta :

solve(
    [
        Eq(z, sin(theta)),
        Eq(z_o, cos(theta))
    ],
    [z_o, theta],
    dict=True
)

which yields

res

You can then throw away the result for theta and use the rest.

This doesn't work for all situations - it requires that the intermediate variable be something that sympy could solve for directly.

Eliminate a variable to relate two functions in Python using SymPy

3 Answers3