structuring binary data for sankey plot

Question

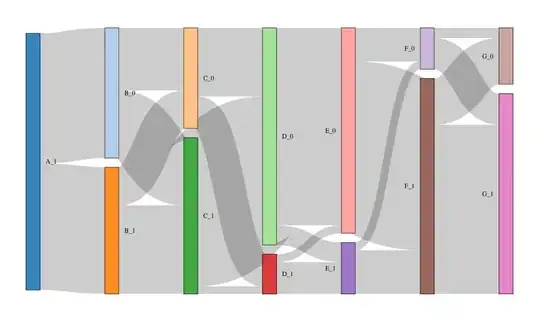
I am having trouble figuring out how to make a sankey plot for data where there are multiple opportunities of success (1) or failure (0). You can generate my sample with the following code:

# example
library(networkD3)
library(tidyverse)
library(tidyr)

set.seed(900)
n=1000
example.data<-data.frame("A" = rep(1,n),
                         "B" = sample(c(0,1),n,replace = T),
                         "C" = rep(NA,n),
                         "D" = rep(NA,n),
                         "E" = rep(NA,n),
                         "F" = rep(NA,n),
                         "G" = rep(NA,n))

for (i in 1:n){
  example.data$C[i]<- ifelse(example.data$B[i]==1,
                                   sample(c(0,1),1,prob = c(0.3,0.7),replace = F),
                                   sample(c(0,1),1,prob = c(0.55,0.45),replace = F))
  example.data$D[i]<-ifelse(example.data$C[i]==1,
                                              sample(c(0,1),1,prob = c(0.95,0.05),replace = F),
                                              sample(c(0,1),1,prob = c(0.65,0.35),replace = F))
  example.data$E[i]<-ifelse(example.data$C[i]==0 & example.data$D[i]==0,
                                    sample(c(0,1),1,prob = c(.9,.1),replace = F),
                                    ifelse(example.data$C[i]==0 & example.data$D[i]==1,
                                           sample(c(0,1),1,prob = c(.3,.7),replace = F),
                                           ifelse(example.data$C[i]==1 & example.data$D[i]==0,
                                                  sample(c(0,1),1,prob = c(.9,.1),replace = F),
                                                  sample(c(0,1),1,prob = c(.1,.9),replace = F))))
  example.data$F[i]<-ifelse(example.data$E==1,
                                         sample(c(1,0),1,prob=c(.85,.15),replace = F),
                                         sample(c(1,0),1,prob = c(.01,.99),replace = F))
  example.data$G[i]<-sample(c(1,0),1,prob = c(.78,.22),replace = F)
}


example.data.1<-example.data%>%
  gather()%>%
  mutate(ORDER = c(rep(0,n),rep(1,n),rep(2,n),rep(3,n),rep(4,n),rep(5,n),rep(6,n)))%>%
  dplyr::select("Event" = key,
                "Success" = value,
                ORDER)%>%
  group_by(ORDER)%>%
  summarise("YES" = sum(Success==1),
            "NO" = sum(Success==0))

The tricky part for me is how I can generate the links data without having to manually specify the source targets and values.

I used the sankey example from this website, and proceeded to muscle my own example data in the least elegant way possible:

links<-data.frame("source" = sort(rep(seq(0,10,1),2)),
           "target" = c(1,2,3,4,3,4,5,6,5,6,7,8,7,8,9,10,9,10,11,12,11,12),
           "value" = c(sum(example.data$A==1 &example.data$B==1), #1
                       sum(example.data$A==1 & example.data$B==0),#2
                       sum(example.data$B==1 & example.data$C==1),#3
                       sum(example.data$B==1 & example.data$C==0),#4
                       sum(example.data$B==0 & example.data$C==1),#5
                       sum(example.data$B==0 & example.data$C==0),#6
                       sum(example.data$C==1 & example.data$D==1),#7
                       sum(example.data$C==1 & example.data$D==0),#8
                       sum(example.data$C==0 & example.data$D==1),#9
                       sum(example.data$C==0 & example.data$D==0),#10
                       sum(example.data$D==1 & example.data$E==1),#11
                       sum(example.data$D==1 & example.data$E==0),#12
                       sum(example.data$D==0 & example.data$E==1),#13
                       sum(example.data$D==0 & example.data$E==0),#14
                       sum(example.data$E==1 & example.data$F==1),#15
                       sum(example.data$E==1 & example.data$F==0),#16
                       sum(example.data$E==0 & example.data$F==1),#17
                       sum(example.data$E==0 & example.data$F==0),#18
                       sum(example.data$F==1 & example.data$G==1),#19
                       sum(example.data$F==1 & example.data$G==0),#20
                       sum(example.data$F==0 & example.data$G==1),#21
                       sum(example.data$F==0 & example.data$G==0)))#22

nodes<-data.frame("name" = names(example.data))


example.list<-list(nodes,links)

names(example.list)<-c("nodes","links")

My problem is this. 1) trying to use this data in the sankeyNetwork function does not actually produce a plot at all, and 2) Obviously this method will be prone to a lot of error especially if there are more than 2 targets per node.

I found an example on stack where the person used the match call in a dplyr::mutate function that looked promising for what I'm trying to accomplish, but the data had a slightly different structure and I did't really know how to get the match call to work with my own data.

The output I'm going for is a sankey plot that shows the number of observations moving between each of the events/outcomes [A:F]. So imagine each of the columns represent an event either successful or not successful. The sakey plot would illustrate a summary of total successes and failures of each event. So all 1000 observations starting at A with 493 going to a node of B = 1, and the remaining 507 going to the node indicating B = 0. Of the 493 in B = 1, 345 go to the node indicating C = 1, and 148 go to the node C = 0. Of the 507 in B = 0 263 go to C = 1 and 244 go to C = 0, and so on for the rest of the event A through F. I hope I've made this clear enough. Any help on this would be greatly appreciated.

@CJ Thanks for the help on the first part. To clarify the plot I'm looking for, imagine all 1000 observations walk through 1 of 2 doors labeled YES or NO for each of the column variables. So, all 1000 start at A and walk through either B = YES or B = NO. Next, all 1000 walk through C= YES or C = NO. Next, all 1000 walk through D= YES or D = NO, etc — slap-a-da-bias, Oct 19 '18 at 16:33

CJ Yetman · Accepted Answer · 2018-10-19T21:50:39.870

The sankey plot does not work because you refer to nodes in you target and source columns that don't exist in your nodes data frame.

to demonstrate...

sort(unique(c(links$source, links$target)))
# [1]  0  1  2  3  4  5  6  7  8  9 10 11 12

nrow(nodes)
# [1] 7

To reshape your original data into the proper format...

The reason your original data is difficult to work with is because important information that you want to use is implicitly encoded in the shape of your data, but not explicitly included in the data. Each data point in a given row have an implicit relationship that they were chosen by the same entity, but that information does not exist explicitly in your data. Likewise, each column implicitly represents one of a sequential chain of actions. A good test for this situation is to ask yourself if you reshaped the data, or sorted it by a column, or reordered the columns, would you still have the same information? If you swapped column B for column D, would you still have all the same information? Ignoring the fact that one could implicitly assume the intended order of your columns because they are named in alphabetical order, the answer is no... so that's where you need to start, by encoding that information into your data.

Add the row number as a variable/column, then gather all the columns into long format, and add the column number...

events <- 
  example.data %>% 
  as_tibble() %>% 
  mutate(row = row_number()) %>% 
  gather(column, choice, -row) %>% 
  mutate(column_num = match(column, names(example.data))) %>% 
  arrange(row, column_num) %>% 
  select(row, column_num, everything())

events
# # A tibble: 7,000 x 4
#      row column_num column choice
#    <int>      <int> <chr>   <dbl>
#  1     1          1 A           1
#  2     1          2 B           1
#  3     1          3 C           1
#  4     1          4 D           0
#  5     1          5 E           1
#  6     1          6 F           1
#  7     1          7 G           0
#  8     2          1 A           1
#  9     2          2 B           0
# 10     2          3 C           1
# # ... with 6,990 more rows

Now the data represents one event/choice per row, with all the critical info you need. In your desired output, each "node" is defined by the column and a choice made at that stage... so A_1, B_0, B_1, C_0, C_1, etc. For each event in your reshaped data, you want to know at which node that choice/event took place ("target"), and which node was it coming from ("source"). The target node is the column name and the choice of that event. The source node is the column name and choice of the event that preceded it (-1 column_num) within the same row (person/entity/observation).

links <-
  events %>% 
  mutate(target = paste0(column, "_", choice)) %>% 
  group_by(row) %>% 
  mutate(source = lag(target)) %>% 
  filter(!is.na(source) & !is.na(target))

links
# # A tibble: 6,000 x 6
# # Groups:   row [1,000]
#      row column_num column choice target source
#    <int>      <int> <chr>   <dbl> <chr>  <chr> 
#  1     1          2 B           1 B_1    A_1   
#  2     1          3 C           1 C_1    B_1   
#  3     1          4 D           0 D_0    C_1   
#  4     1          5 E           1 E_1    D_0   
#  5     1          6 F           1 F_1    E_1   
#  6     1          7 G           0 G_0    F_1   
#  7     2          2 B           0 B_0    A_1   
#  8     2          3 C           1 C_1    B_0   
#  9     2          4 D           0 D_0    C_1   
# 10     2          5 E           1 E_1    D_0   
# # ... with 5,990 more rows

Now you want to summarize that data. You want to count the number of each unique link/path.

links <- 
  links %>% 
  select(source, target) %>% 
  group_by(source, target) %>% 
  summarise(value = n()) %>% 
  ungroup()

links
# # A tibble: 22 x 3
#    source target value
#    <chr>  <chr>  <int>
#  1 A_1    B_0      507
#  2 A_1    B_1      493
#  3 B_0    C_0      244
#  4 B_0    C_1      263
#  5 B_1    C_0      148
#  6 B_1    C_1      345
#  7 C_0    D_0      267
#  8 C_0    D_1      125
#  9 C_1    D_0      579
# 10 C_1    D_1       29
# # ... with 12 more rows

With that, you just need to put it in the format that sankeyNetwork requires... a nodes data frame with one row for each unique node, and a links data frame where the source and target columns are numeric and refer to the index (0-based) of the nodes in the nodes data frame (the row nunber they appear on - 1).

nodes <- data.frame(name = unique(c(links$source, links$target)))

links$source <- match(links$source, nodes$name) - 1
links$target <- match(links$target, nodes$name) - 1

sankeyNetwork(Links = links, Nodes = nodes, Source = "source", 
              Target = "target", Value = "value", NodeID = "name")

Thank you so much! Not to get personal, but it's been a rough day and this was the one thing that ended well. I'd shake your hand if I could — slap-a-da-bias, Oct 19 '18 at 23:07

structuring binary data for sankey plot

1 Answers1

Linked