This a variant of subset sum problem, or more generally, the Knapsack problem. The following solution supposes that:
- All elements of the initial array are strictly positive,
- The initial array may contain repeating elements,
- If a sum can't be reached, the output is an empty array.
Let's starts with an example: let's create a dynamic table in which we'll try to find all the ways to get 5 by adding elements from [1, 2, 3, 4]:

In this table, the rows represent the elements of the array, in an ascending order, plus 0. The columns go from 0 to the sum 5.
In each cell, we ask ourselves, can we get to the title of this column, by adding one or more of the titles of the current and previous rows.
The number of solutions is the count of cells having true in them. In this case, two solutions:
1)
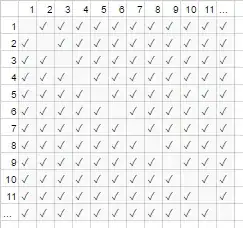
The green cell is true, so the current line is the last element from the solution. In this case, 3 is part of the solution. So the problem of finding a subarray which sum is 5, becomes finding a subarray which sum is 5 - 3. Which is 2. This is represented by the purple arrow 1: Go five columns to the left, and 1 row up.
In arrow 2, we look for the subset that has made it possible to have a partial sum of 2. In this case, we get two thanks to the 2 element. So following arrow 2 we go one row up, and two to the left.
With arrow 3 we reach the first cell in the first column, corresponding to 5 - 3 - 2, which is 0.
2)
Another path we could take starts from the red cell:
As you can see, the problem of making 5 out of [1, 2, 3, 4], becomes a new smaller problem of making 1 from [1, 2, 3], and then 1 out of [1, 2], and finally 1 out of `1.
Let's create and fill the dynamic table:
var dynamicTable: [[Bool]] =
Array(repeating: Array(repeating: false, count: sum + 1),
count: array.count + 1)
//All of the elements of the first column are true
//since we can always make a zero sum out of not elements
for i in 0...array.count {
dynamicTable[i][0] = true
}
for row in 1...array.count {
for column in 1...sum {
if column < array[row - 1] {
dynamicTable[row][column] = dynamicTable[row - 1][column]
} else {
if dynamicTable[row - 1][column] {
dynamicTable[row][column] = true
} else {
dynamicTable[row][column] = dynamicTable[row - 1][column - array[row - 1]]
}
}
}
}
Let's find all the paths leading to the sum:
var solutions = [[Int]]()
func getSubArraysWithTheSum(arr: [Int], row: Int, currentSum: Int, currentSolution: [Int]) {
//The following block will be executed when
//we reach the first cell in the first column
if row == 0,
currentSum == 0
{
solutions.append(currentSolution)
//notice the return to exit the scope
return
}
//The following block will be executed if
//the current cell is NOT used to reach the sum
if dynamicTable[row - 1][currentSum]
{
getSubArraysWithTheSum(arr: arr,
row: row - 1,
currentSum: currentSum,
currentSolution: currentSolution)
}
//The following block will be executed if
//the current cell IS used to reach the sum
if currentSum >= arr[row - 1],
dynamicTable[row - 1][currentSum - arr[row - 1]]
{
getSubArraysWithTheSum(arr: arr,
row: row - 1,
currentSum: currentSum - arr[row - 1],
currentSolution: currentSolution + [arr[row - 1]])
}
}
The whole function looks like this:
func getSubArrays(from array: [Int], withSum sum: Int) -> [[Int]] {
guard array.allSatisfy({ $0 > 0 }) else {
fatalError("All the elements of the array must be strictly positive")
}
guard array.count > 0, sum > 0 else {
return []
}
var solutions = [[Int]]()
var dynamicTable: [[Bool]] =
Array(repeating: Array(repeating: false, count: sum + 1),
count: array.count + 1)
//All of the elements of the first column are true
//since we can always make a zero sum out of not elements
for i in 0...array.count {
dynamicTable[i][0] = true
}
for row in 1...array.count {
for column in 1...sum {
if column < array[row - 1] {
dynamicTable[row][column] = dynamicTable[row - 1][column]
} else {
if dynamicTable[row - 1][column] {
dynamicTable[row][column] = true
} else {
dynamicTable[row][column] = dynamicTable[row - 1][column - array[row - 1]]
}
}
}
}
func getSubArraysWithTheSum(arr: [Int], row: Int, currentSum: Int, currentSolution: [Int]) {
//The following block will be executed when
//we reach the first cell in the first column
if row == 0,
currentSum == 0
{
solutions.append(currentSolution)
return
}
//The following block will be executed if
//the current cell is NOT used to reach the sum
if dynamicTable[row - 1][currentSum]
{
getSubArraysWithTheSum(arr: arr,
row: row - 1,
currentSum: currentSum,
currentSolution: currentSolution)
}
//The following block will be executed if
//the current cell IS used to reach the sum
if currentSum >= arr[row - 1],
dynamicTable[row - 1][currentSum - arr[row - 1]]
{
getSubArraysWithTheSum(arr: arr,
row: row - 1,
currentSum: currentSum - arr[row - 1],
currentSolution: currentSolution + [arr[row - 1]])
}
}
getSubArraysWithTheSum(arr: array, row: array.count , currentSum: sum, currentSolution: [])
return solutions
}
Here are some test cases:
getSubArrays(from: [3, 1, 4, 2], withSum: 5) //[[3, 2], [4, 1]]
getSubArrays(from: [1, 2, 2, 4], withSum: 3) //[[2, 1], [2, 1]]
getSubArrays(from: [7, 3, 4, 5, 6, 1], withSum: 9) //[[5, 3, 1], [5, 4], [6, 3]]
getSubArrays(from: [3], withSum: 3) //[[3]]
getSubArrays(from: [5], withSum: 10) //[]
getSubArrays(from: [1, 2], withSum: 0) //[]
getSubArrays(from: [], withSum: 4) //[]
This solution has been inspired by Sumit Ghosh's contribution here. A thorough explanation of how the dynamic table is constructed can be found in this video.


