OpenGL ES GLSL Mandelbrot with general exponent

Question

I have successfully implemented several fractals on GLSL(OpenGL ES), but I seem to be getting nowhere with the variation of Mandelbrot set where the exponent is an arbitrary positive number.

I am doing the exponentiation in complex polar coordinates, but the algorithm is wrong somewhere, as for exponent = 2 something else than the classical Mandelbrot set appears.

The current code is as follows:

precision mediump float;

uniform sampler2D palette;
uniform float centerX;
uniform float centerY;
uniform float scale;
uniform float iterations;
uniform vec2 resolution;
uniform float exponent;
#define maxiter 65535

vec2 cplx_polar(vec2 z) {
    return vec2(length(z), atan(z.y,z.x));
}

vec2 cplx_polar_add(vec2 z1, vec2 z2) {
    //https://math.stackexchange.com/a/1365938
    return vec2(sqrt(z1.x*z1.x + z2.x*z2.x + 2.*z1.x*z2.x*cos(z2.y-z1.y)),
    z1.y+atan(z2.x*sin(z2.y-z1.y),(z1.x+z2.x*cos(z2.y-z1.y))));
}

vec2 exponentiate(vec2 z) {
    return pow(z.x, exponent)* vec2(cos(z.y), sin(z.y));
}

void main() {
    vec2 center = vec2(centerX, centerY);
    vec2 coord = vec2(gl_FragCoord.x, gl_FragCoord.y) / resolution;
    vec2 c = cplx_polar((coord - center) / scale);
    int j = 0;
    vec2 z = c;
    for(int i = 0; i<maxiter; i++) {
        if (float(i) >= iterations) break;
        j++;
        vec2 znew = cplx_polar_add(exponentiate(z), c);
        if(znew.x > 2.0) break;
        z = znew;
    }
    gl_FragColor = texture2D(palette, vec2((j == int(iterations) ? 0.0 : float(j)) / iterations, 0.5));
}

There must be a mistake in the main function as basically the same works for the simple z = z ^ 2 + c without polar coordinates. The generated image for exponent = 2 looks like

while it should look like

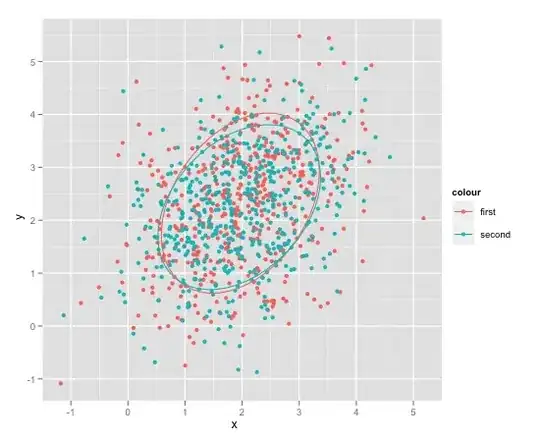I am at a loss. It may be something trivial. I would be grateful for any advice.

Answer 1

I'm not sure about using polar calcs for so simple an interation calc, it seems a bit overkill to me. Here is a solution using cartesian maths derived from my FractalCanvas app.

The simple expression in Java is pow(double f) { return log().times(f).exp(); }.

I don't recognise the language you are using, but this could provide some ideas.

public vec2 pow(vec2 z, double f) {
    // log()
    double d = Math.log(Math.sqrt(z.x * z.x + z.y * z.y));
    z.x = Math.atan2(z.y, z.x);
    z.y = d;
    // times(f)
    z.x *= f;
    z.y *= f;
    // exp()
    double exp = Math.exp(z.x);
    z.x = Math.cos(z.y) * exp;
    z.y = Math.sin(z.y) * exp;
    return z;
}

BTW I seriously suggest you don't create objects in the middle of an iteration loop. Creating and destroying them takes finite time and the loop may be run billions of times to calculate an image. When I removed such creations from my app, I noticed a substantial speedup.