2

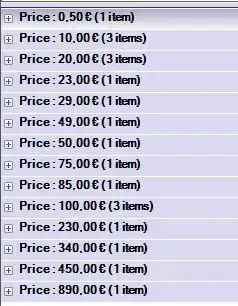
I have two pairs of data sets, x1 vs y1 and x2 vs y2. x1, y1, x2, y2 all have uneven distribution of data represented by the following images:

x1 x2 y1 y2

My problem is to determine the intersection of the two pairs of data sets, x1/y1 and x2/y2, shown in following image:

x1/y1 vs x2/y2

I tried interpolating the data points to have even spacing, but due invalid regions of x1/y1 where there are multiple solutions for the same x value.

Here is a zoom in of the x1/y1 and x2/y2 relationship, showing that there are knots within the data set that cannot be interpolated in any orientation:

zoom in of x1/y1 and x2/y2 relationship

Andras Deak -- Слава Україні
  • 33,737
  • 11
  • 83
  • 111
John CAE
  • 21
  • 3
  • Looking at the last image, it appears that if you switch the `x` and `y` **of the plot** (imagine transposing the image) you would get curves that are suitable for interpolation.... Did you try that? – Dev-iL Oct 07 '18 at 14:42
  • I have, but there are also multiple solutions for the y values, which also made the interpolation incredibly unstable. – John CAE Oct 07 '18 at 15:08
  • Seeing how you said that your problem was the intersections of the curves in the last image, and if you switch the horizontal and vertical axes in that image the problem appears to go away (according to me) - I'm no longer sure what the problem is... – Dev-iL Oct 07 '18 at 15:10
  • I just added a zoomed in image of the x1/y1 vs x2/y2 plot. There are knots within the x1/y1 data set that cannot be interpolated in any orientation. – John CAE Oct 07 '18 at 15:17
  • Is runtime a problem? You can just pairwise check every line segment against each other to see which subsegments intersect. It's slow, but you could speed it up with heuristics like only checking against the segments with the closest points. – user3658307 Oct 07 '18 at 15:23
  • I see what you mean. Did you try filtering it? Averaging/binning? Replacing values by uniques with tolerance (`uniquetol`)? – Dev-iL Oct 07 '18 at 15:24
  • Yea, I see how checking line segments against each other would work, I can try that and see how long it would take. I have tried running averages, a bunch of different fits and lowpass filtering. Didn't really like the results as they deviated too much from the original data. – John CAE Oct 07 '18 at 15:31
  • Interesting problem. Did you try to use the polygon functionality in MATLAB? It’s quite new, you need a release from the last few years I believe. But you could think of these lines as polygons, and look for intersection points. – Cris Luengo Oct 07 '18 at 18:33
  • You have non monotonic data, so you can't interpolate your data without a small transformation. To interpolate the x1/y1 data you can try to use this small trick. `t = [0,cumsum(sqrt(diff(x1).^2+diff(y1).^2))]; ti = linspace(0,t(end),2000); x = interp1(t,x1,ti); y = interp1(t,y1,ti);` – obchardon Oct 08 '18 at 08:47

1 Answers1

1

It seems that x2/y2 is a smooth curve, so you should be able to interpolate it piecewise with polynomials, and get decent results. Of course you will not want to do this with x1/y1, as your data is crazy. I will refer to the independent variable in the last two images as t. You can use the matlab spline function to do this interpolation from arrays of t and x2/y2 values. Your t value array in this case should be the same size as your set of x2/y2 values. Then you could loop over your x1/y1 points, using the interpolation to estimate x2/y2 at the same value of t. Then you could subtract these values. When the sign of this value changes for two consecutive x1/y1 points, you have a point of intersection between them. Then perform a linear interpolation between those two x1/y1 points and find the intersection of that line with your interpolated x2/y2 function. The code may get a little messy, but it should work. You will want to look at the MATLAB spline documentation.

HackerBoss
  • 829
  • 7
  • 16