Performing a reflective center pad on an image

Question

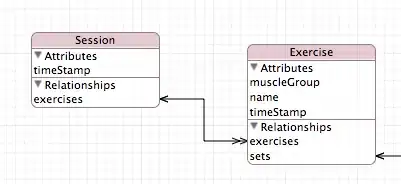
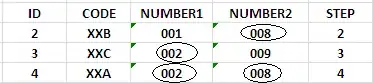
This forum thread from an active Kaggle competition mentions something the author calls a "reflective center pad". Basically this is a transformation that takes the edges of the image and reflects them outwards, causing mirroring on the edges of the image, which the author shows slightly but noticeably improves model performance.

For reference, here is the image they post demonstrating this technique:

My question is twofold:

Does this transformation have a canonical name? "Reflective center pad" sounds unofficial.
What's a simple way of expressing this transformation in code, perhaps using numpy and something like skimage?

@Eric and much faster than mine, too. I'm semi-surprised. Yes, mine does the expensive fancy indexing. OTOH, I've been conditioned to expect those little numpy convenience functions to come with ginormous overheads. — Paul Panzer, Sep 24 '18 at 15:11

score 6 · Accepted Answer · answered Sep 24 '18 at 08:31

Does this transformation have a canonical name? "Reflective center pad" sounds unofficial.

"Symmetric padding" is a commonly used expression to refer to this transformation.

What's a simple way of expressing this transformation in code

I think the simplest way to achieve that would be using Numpy's pad with mode='symmetric'.

Demo

import numpy as np
from skimage import data
import matplotlib.pyplot as plt

img = data.astronaut()
padded = np.pad(img, pad_width=((100, 200), (100, 500), (0, 0)), mode='symmetric')

fig, (ax1, ax2) = plt.subplots(2, 1)
ax1.imshow(img)
ax2.imshow(padded)
fig.show()

Choose carefully between `reflect` and `symmetric` – Eric Sep 24 '18 at 21:07 — Eric, Sep 24 '18 at 21:07

score 4 · Answer 2 · answered Sep 24 '18 at 04:11

To answer your 2nd question:

import Image
import numpy as np
from scipy.misc import face

# example input
f = face()[200:500:2, 400:800:2]
# example output size
outy, outx = 480, 640

iny, inx, *_ = f.shape
iny -= 1; inx -= 1
yoffs, xoffs = (outy - iny) // 2, (outx - inx) // 2

Y, X = np.ogrid[:outy, :outx]
# transformation logic is essentially contained in line below
out = f[np.abs((Y - yoffs + iny) % (2*iny) - iny), np.abs((X - xoffs + inx) % (2*inx) - inx)]

Image.fromarray(out).save('m.png')

Result:

Performing a reflective center pad on an image

2 Answers2

Demo