How To simplify boolean equations

Question

Note that this is an example question to represent the sum of all similar questions, please don't answer only the question below, but the general problem with optimizing boolean expressions

I have this boolean Equation:[boolean equation] e.g. (!B && A) || A

is there any better way for this?

You can use following sequence for better performance A || (!B && A) — mcacorner, Sep 12 '18 at 07:34
This question is not about how to simplify that single equation but in general — Scorix, Sep 12 '18 at 07:35
Does this answer your question? [Simplify boolean expression algorithm](https://stackoverflow.com/questions/5311099/simplify-boolean-expression-algorithm) — ggorlen, Oct 21 '20 at 17:39

score -1 · Accepted Answer · edited Jun 20 '20 at 09:12

A boolean equation follows simple calculations rules, known as the Boolean Algebra.

With those rules, you can simplify any boolean equation with hard work:

 Associativity of ∨ :         x ∨ ( y ∨ z ) = ( x ∨ y ) ∨ z 
 Associativity of ∧ :         x ∧ ( y ∧ z ) = ( x ∧ y ) ∧ z
 Commutativity of ∨ :                 x ∨ y = y ∨ x 
 Commutativity of ∧ :                 x ∧ y = y ∧ x 
 Distributivity of ∧ over ∨ : x ∧ ( y ∨ z ) = ( x ∧ y ) ∨ ( x ∧ z )
 Identity for ∨ :                     x ∨ 0 = x
 Identity for ∧ :                     x ∧ 1 = x 
 Annihilator for ∧ :                  x ∧ 0 = 0 

 The following laws hold in Boolean Algebra, but not in ordinary algebra:

 Annihilator for ∨ :                  x ∨ 1  = 1
 Idempotence of ∨ :                    x ∨ x = x 
 Idempotence of ∧ :                    x ∧ x = x  
 Absorption 1:                 x ∧ ( x ∨ y ) = x  
 Absorption 2:                 x ∨ ( x ∧ y ) = x 
 Distributivity of ∨ over ∧ : x ∨ ( y ∧ z ) = ( x ∨ y ) ∧ ( x ∨ z )

 Complementation 1 :                  x ∧ ¬x = 0
 Complementation 2 :                  x ∨ ¬x = 1
 Double negation :                     ¬(¬x) = x
 De Morgan 1 :                       ¬x ∧ ¬y = ¬(x ∨ y)
 De Morgan 2 :                       ¬x ∨ ¬y = ¬(x ∧ y)

Note that

∨ represents OR (||)
∧ represents AND (&&)
¬ represents NOT (!)
= represents EQUALS (==)

But with more complexity of your equation, this done by hand is almost impossible. The first step to the completion is the truth table. It should look something like this:

You can create truth tables also online, for example with this tool.

From the truth table, you can create a KV-Map. Those can look like this:

There also online tools to create KV-Maps (I recommend this one)).

How to fill in those maps according to your truth table is not the topic here.

How to get boolean equations from the KV-Map is also not the topic, but the recommended tool is calculating it for you:

In conclusion for the problem: if you want to optimize your boolean equations, create a truth table with your equation:

Fill in a KV-Map:

and replace your equation with the calculated shortest way possible:

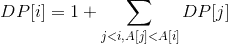
Supplement: the equation calculated with the KV-Map is the shortest way possible. There are still some transformations you can do with the boolean algebra, but that will not make these equations look easier.

How To simplify boolean equations

1 Answers1