0

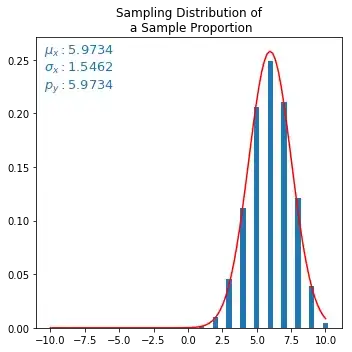
I was trying to simulate "Sampling Distribution of Sample Proportions" using Python. I tried with a Bernoulli Variable as in example here

The crux is that, out of large number of gumballs, we have yellow balls with true proportion of 0.6. If we take samples (of some size, say 10), take mean of that and plot, we should get a normal distribution.

I have managed to obtain the sampling distribution as normal, however, the actual normal continuous curve with same mu and sigma, does not fit at all, but scaled to few factors up. I am not sure what is causing this, ideally it should fit perfectly. Below is my code and output. I tried varying the amplitude and also sigma (dividing by sqrt(samplesize)) but nothing helped. Kindly help.

Code: 

from SDSP import create_bernoulli_population, get_frequency_df
from random import shuffle, choices
from bi_to_nor_demo import get_metrics, bare_minimal_plot
import matplotlib.pyplot as plt


N = 10000  # 10000 balls
p = 0.6    # probability of yellow ball is 0.6, and others (1-0.6)=>0.4
n_pickups = 10       # sample size
n_experiments = 2000  # I dont know what this is called 


# STATISTICAL PDF
# choose sample, take mean and add to X_mean_list. Do this for n_experiments times. 
X_hat = []
X_mean_list = []
for each_experiment in range(n_experiments):
    X_hat = choices(population, k=n_pickups)  # choose, say 10 samples from population (with replacement)
    X_mean = sum(X_hat)/len(X_hat)
    X_mean_list.append(X_mean)
stats_df = get_frequency_df(X_mean_list)


# plot both theoretical and statistical outcomes
fig, ax = plt.subplots(1,1, figsize=(5,5))
from SDSP import plot_pdf
mu,var,sigma = get_metrics(stats_df)
plot_pdf(stats_df, ax, n_pickups, mu, sigma, p=mu, bar_width=round(0.5/n_pickups,3),
         title='Sampling Distribution of\n a Sample Proportion')
plt.tight_layout()
plt.show()

Output:
Red curve is the misfit normal approximation curve. The mu and sigma is derived from statistical discrete distribution (small blue bars), and fed to formula calculating normal curve. But normal curve looks scaled up somehow.
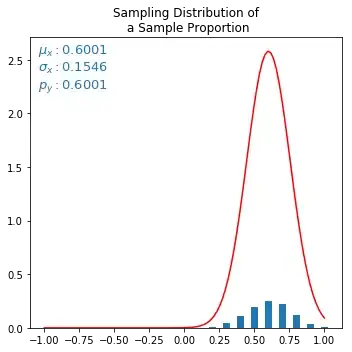
output image

Update:
Avoiding a division to take average, solves the graph issue but mu is scaled. So issue is still not fully solved yet. :(

X_mean = sum(X_hat) # removed the division /len(X_hat)

Output after removing above division (but its needed?):
output

Parthiban Rajendran
  • 430
  • 1
  • 7
  • 18
  • The mean looks to be close to 0.6, which is the true mean proportion. What's wrong with mu in your problem? – Joel Aug 07 '18 at 17:57
  • Oh sorry, I meant red graph, not red legend. Both discrete and continuous have same mean and sigma as noted in graph, but the red curve somehow is not fitting with discrete one, but looks scaled up. – Parthiban Rajendran Aug 07 '18 at 18:09
  • The area between the red curve and the x-axis must be 1, since it covers everything in the event space. The blue bars, however, must sum 1. The red curve represents probability density, and if you look at the area between the red curve and the x-axis, it looks to be approximately (if not exactly) 1. With the blue bars, it appears that their sum is 1 upon first glance. I think your issue is a general problem when graphing discrete and continuous distributions simultaneously. – Joel Aug 07 '18 at 18:15
  • If that is the case, how do we say, its a good approximation of discrete distribution underneath? I even tried np >= 30 with n=50, p=0.6, the gap only worsens like [this](https://s22.postimg.cc/wil3rnlap/image.png), red curve going farther away. Also any way we could show normal curve fits approximately on discrete by increasing the blue bars? Its not visually convincing currently. I tried increasing n_experiments, n_pickups (sample size), but in vain. – Parthiban Rajendran Aug 07 '18 at 18:20
  • It won't be visually appealing, and that's the point. Perhaps graphing these two plots simultaneously is not a good way to visualize the data due to the discrepancies in y-axis values. – Joel Aug 07 '18 at 18:32
  • I just found a glitch I guess, and seems to be correcting the graph, will revert soon. – Parthiban Rajendran Aug 07 '18 at 18:32
  • But but but, now graph is good, but my mu is appearing scaled. aargh. – Parthiban Rajendran Aug 07 '18 at 18:47

0 Answers0