I have a webcam looking down on a surface which rotates about a single-axis. I'd like to be able to measure the rotation angle of the surface.
The camera position and the rotation axis of the surface are both fixed. The surface is a distinct solid color right now, but I do have the option to draw features on the surface if it would help.
Here's an animation of the surface moving through its full range, showing the different apparent shapes:
My approach thus far:
- Record a series of "calibration" images, where the surface is at a known angle in each image
- Threshold each image to isolate the surface.
- Find the four corners with cv2.approxPolyDP(). I iterate through various epsilon values until I find one that yields exactly 4 points.
- Order the points consistently (top-left, top-right, bottom-right, bottom-left)
- Compute the angles between each points with atan2.
- Use the angles to fit a sklearn linear_model.linearRegression()
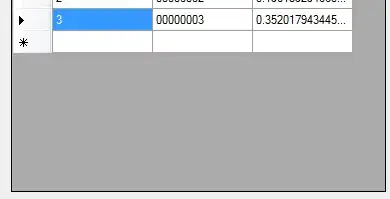
This approach is getting me predictions within about 10% of actual with only 3 training images (covering full positive, full negative, and middle position). I'm pretty new to both opencv and sklearn; is there anything I should consider doing differently to improve the accuracy of my predictions? (Probably increasing the number of training images is a big one??)
I did experiment with cv2.moments directly as my model features, and then some values derived from the moments, but these did not perform as well as the angles. I also tried using a RidgeCV model, but it seemed to perform about the same as the linear model.