Binomial Test in SAS and R - Different Results

Question

I need to replicate a binomial test from R to SAS but I'm obtaining different results (or maybe I am misinterpreting the SAS results).

In order to explain my problem in an easy way, I will use data from this wikipedia example because it provides the final solution;

Suppose you want to calculate the probability of obtaining 51 or more 6s in a sample of 235 roll of a fair die with 6 faces, so that the true probability of rolling a 6 on each trial is 1/6. The final solution should be 0.02654.

In R, the code to do is the following:

binom.test(51,235,(1/6),alternative = "greater")

and the obtained results are:

Exact binomial test

data: 51 and 235 number of successes = 51, number of trials = 235,
p-value = 0.02654
alternative hypothesis: true probability of success is greater than 0.1666667
95 percent confidence interval:
0.1735253 1.0000000
sample estimates: probability of success
0.2170213

When in SAS the equivalent should be given by:

DATA DICEROLL;
ROLL=51;
FREQQ=235;
PROB=1/6;
RUN;

data _null_;
set diceroll;
call symput("probability",prob);
run;

PROC FREQ DATA=DiceRoll ;
    TABLES FREQQ / BINOMIAL (P=&probability.) ALPHA=0.05;
    EXACT  BINOMIAL ;
    WEIGHT ROLL ;
RUN;

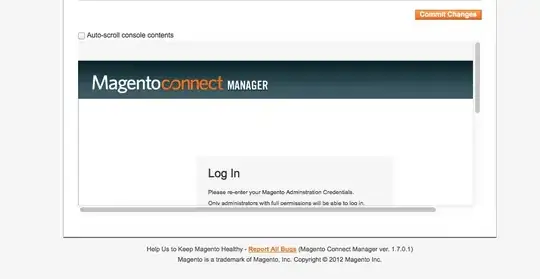
But THIS is the results I obtain (in which there is no p-value = 0.02654)

I tried in several ways to reconcile my results(tried all the three alternatives in R, tried to invert ROLL and FREQQ in sas because I wasn't sure) but I still haven't found a solution. Do binom.test and proc freq + BINOMIAL perform at least the same test? Am I misinterpreting the SAS output?

Thank you in advance for you precious help!

============================== UPDATE ============================

I tried both proposed methodology by reeza and BEMR and I feel I am close to the solution! @BEMR: as I wrote and explained bettere in the comment, how should I adapt %r(1,6) if my variable is dichotomic? Your code works with the example of a 6-faced die but in my real case, my success variable assume values between 0 and 1, so I am not sure of what I have to do (I apologize if I did not mention it at the beginning)

@REEZA: Your solution seems to work but I had to remove the /2; I guess your first solution calculates p-values as a two sided test not one sided. Anyway, the results are fine but there are huge differences between SAS and R when the number of success is 0 or close to 0 (1,2,3). Do you know any workaround for this? Or better, is it safe to assume that the test is unreliable in both cases? The following pictures are my results with the reeza method, thank you all for your precious cooperation!

Answer 1

You obviously don't need to have the variables set up this way, but this more of a one to one type comparison. SAS doesn't have the capacity to do a one sided test that I saw within the function but I didn't read up much on it or try and figure if it's right. But this the type of approach you should be using in SAS to get similar numbers, not PROC FREQ.

    data demo;
nSuccesses=51;
prob_success=1/6;
nTrials = 235;

y=(1-cdf('BINOM', nsuccesses, prob_success, ntrials))/2;
run;

proc print data=demo;
run;

http://documentation.sas.com/?docsetId=lefunctionsref&docsetTarget=p1cxa81efqtsszn12ueyitll9esw.htm&docsetVersion=9.4&locale=ja#p03dt2kdzjjucxn198ytlpnrf1r4

Answer 2

If you wanted to compare binom.test and proc freq + BINOMIAL you could using a simulation in SAS. The following code provides an example:

When the dice is rolled 235 and the result can be 1,...,6.

*Create df: random roll;
*macro: random int between min and max;;
  %macro r(min,max);
(&min + floor((1+&max-&min)*rand("uniform"))) 
   %mend;
  data df;
  f = 0;
  do i = 1 to 235; *number of trials;
    x = %r(1,6); *call macro %r() to generate random number between 1,...,6; 
if x = 6 then f = f + 1; *if the random number = 6, add freq from the previous;
relative = f/i; *relative freq;
 output;
end;
run;

*plot relative freq, reference line (1/6), probability of rolling 6;
symbol v=dot c=red;
proc gplot data=df;
plot relative * i/overlay vref=0.16666667 href=500 lh=3;
run;
quit;

This follows an example from here: http://www.stat.purdue.edu/~lfindsen/stat503/Lab2.pdf

*exact binomial using proc freq and simulated data; 
*test if simulation is different from the hypothized 1/6;
proc freq data = df;
tables x / binomial (level=6 p=.166667); 
exact binomial;
run;

When 51 cases are 6 out of the 235.

*Create df2: assign approx 51 cases of 235 a roll of 6;
 data df2;
 do i = 1 to 235; *number of trials;
x = %r(1,5); 
 output;
 end;
 run;
 data df2;
  set df2;
    if i <= 51 then x = 6; *assign six to rows 1 to 51; 
  run;

  *exact binomial using proc freq and simulated data; 
  *test if simulation is different from the hypothized 1/6;
  proc freq data = df2;
tables x / binomial (level=6 p=.166667); 
exact binomial;
  run;

exact binomial one-sided p-value = 0.0265

============================== UPDATE ============================

For the binary variable [0=2184,1=72] instead of using the macro, you could do the following:

    data df3;
    input success n;
    datalines;
    0 2184
    1 72
    ;

    proc freq data=df3;
    weight n; *number of obs for [0,1];
    tables success / binomial (level=2 p=0.509); 
    run;