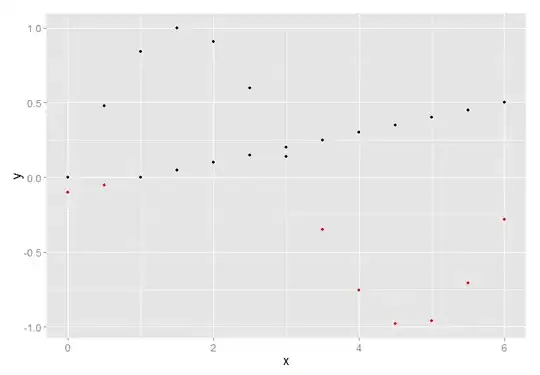
First note that your background removal is almost useless.
If we plot diffI=i2-i1; imshow(diffI,[]);colorbar, we can see that the difference is almost as big as the image itself. You need to understand that what its visually similar to you, its not necessarily similar numerically, and this is a great example for it.

Therefore you dont have what you think you have. The background is there in your thresholding. Then, note that the object you want to segment, its not just whiter. Its definitely as dark as the background in some areas. This means that a simple segmentation by value thresholding will not work. You need better segmentation techniques.
I happen to have a copy of this level set algorithm in my MATLAB, the "Distance Regularized Level Set Evolution".
When I run the code demo_1 with your image, I get the following (nice gif!):

(Uncompressed)
Full code of the demo:
% This Matlab code demonstrates an edge-based active contour model as an application of
% the Distance Regularized Level Set Evolution (DRLSE) formulation in the following paper:
%
% C. Li, C. Xu, C. Gui, M. D. Fox, "Distance Regularized Level Set Evolution and Its Application to Image Segmentation",
% IEEE Trans. Image Processing, vol. 19 (12), pp. 3243-3254, 2010.
%
% Author: Chunming Li, all rights reserved
% E-mail: lchunming@gmail.com
% li_chunming@hotmail.com
% URL: http://www.imagecomputing.org/~cmli//
clear all;
close all;
Img=imread('https://i.stack.imgur.com/Wt9be.jpg');
Img=double(Img(:,:,1));
%% parameter setting
timestep=1; % time step
mu=0.2/timestep; % coefficient of the distance regularization term R(phi)
iter_inner=5;
iter_outer=300;
lambda=5; % coefficient of the weighted length term L(phi)
alfa=-3; % coefficient of the weighted area term A(phi)
epsilon=1.5; % papramater that specifies the width of the DiracDelta function
sigma=.8; % scale parameter in Gaussian kernel
G=fspecial('gaussian',15,sigma); % Caussian kernel
Img_smooth=conv2(Img,G,'same'); % smooth image by Gaussiin convolution
[Ix,Iy]=gradient(Img_smooth);
f=Ix.^2+Iy.^2;
g=1./(1+f); % edge indicator function.
% initialize LSF as binary step function
c0=2;
initialLSF = c0*ones(size(Img));
% generate the initial region R0 as two rectangles
initialLSF(size(Img,1)/2-5:size(Img,1)/2+5,size(Img,2)/2-5:size(Img,2)/2+5)=-c0;
% initialLSF(25:35,40:50)=-c0;
phi=initialLSF;
potential=2;
if potential ==1
potentialFunction = 'single-well'; % use single well potential p1(s)=0.5*(s-1)^2, which is good for region-based model
elseif potential == 2
potentialFunction = 'double-well'; % use double-well potential in Eq. (16), which is good for both edge and region based models
else
potentialFunction = 'double-well'; % default choice of potential function
end
% start level set evolution
for n=1:iter_outer
phi = drlse_edge(phi, g, lambda, mu, alfa, epsilon, timestep, iter_inner, potentialFunction);
if mod(n,2)==0
figure(2);
imagesc(Img,[0, 255]); axis off; axis equal; colormap(gray); hold on; contour(phi, [0,0], 'r');
drawnow
end
end
% refine the zero level contour by further level set evolution with alfa=0
alfa=0;
iter_refine = 10;
phi = drlse_edge(phi, g, lambda, mu, alfa, epsilon, timestep, iter_inner, potentialFunction);
finalLSF=phi;
figure(2);
imagesc(Img,[0, 255]); axis off; axis equal; colormap(gray); hold on; contour(phi, [0,0], 'r');
hold on; contour(phi, [0,0], 'r');
str=['Final zero level contour, ', num2str(iter_outer*iter_inner+iter_refine), ' iterations'];
title(str);