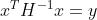The problem that you are solving is an equation that can be expressed as F(x, params) = 0, so it is more natural to use a root-finding function rather than a minimization function. In this case, you have 30 variables and just one equation, so the problem is highly underdetermined, and you would have to deal with that if you used a root-finding function.
The equation defines the level set of a positive definite quadratic form, so you know (as you pointed out) that the set of solutions is an (hyper)ellipsoid. You can take advantage of this structure to easily generate points on the ellipsoid without resorting to a numerical solver.
Three sets of points that are not hard to generate are: the points where the ellipsoid intersects the coordinate axes; the extrema of the ellipsoid relative to the coordinate axes (i.e. the points where a bounding box is tangent to the ellipsoid); and the points where the principal axes of the ellipsoid intersect the ellipsoid. You can also generate random points on the ellipsoid by first generating random points on the unit hypersphere, and then transforming those points to the ellipsoid. This is also demonstrated in the script. Finally, if x is a solution, then so is -x. (That fact is not used in the script.)
Here's a script that creates the sets of points described above. I use 10 variables instead of 30 to limit the amount of printed output.
import numpy as np
from scipy.linalg import sqrtm
from scipy.stats import ortho_group
#--------------------------------------------
# Generate example input
#--------------------------------------------
dim = 10
# Create a positive definite matrix H with shape (dim, dim).
# evals is the vector of eigenvalues of H. This can be replaced
# with any vector of length `dim` containing positive values.
evals = (np.arange(1, dim + 1)/2)**2
# Use a random orthogonal matrix to generate H.
R = ortho_group.rvs(dim)
H = R.T.dot(np.diag(evals).dot(R))
# y determines the level set to be computed.
y = 3.0
#--------------------------------------------
# Compute various points on the ellipsoid
#--------------------------------------------
Hinv = np.linalg.inv(H)
# Ellipsoid intercepts of the coordinate axes
xintercepts = np.diag(np.sqrt(y / np.diag(Hinv)))
# Ellipsoid coordinate extrema
xextrema = H.dot(np.diag(np.sqrt(y / np.diag(H))))
# Ellipsoid intersections with principal axes
evals, evecs = np.linalg.eigh(Hinv)
xprincipal = np.sqrt(y/evals)*evecs
# Generate random points on the ellipsoid.
# The distribution of the random points is not uniform on the ellipsoid.
nsample = 5
r = np.random.randn(H.shape[0], nsample)
# u contains random points on the hypersphere with radius 1.
u = r / np.linalg.norm(r, axis=0)
xrandom = sqrtm(H).dot(np.sqrt(y)*u)
#--------------------------------------------
# Print results
#--------------------------------------------
np.set_printoptions(precision=4, linewidth=120)
print("Columns are the ellipsoid coordinate axis intercepts:")
print(xintercepts)
print("Check:", np.array([x.dot(Hinv.dot(x)) for x in xintercepts.T]))
print()
print("Columns are points where the ellipsoid is tangent to its bounding box:")
print(xextrema)
print("Check:", np.array([x.dot(Hinv.dot(x)) for x in xextrema.T]))
print()
print("Columns are points where the principal axes of the ellipsoid intersect the ellipsoid:")
print(xprincipal)
print("Check:", np.array([x.dot(Hinv.dot(x)) for x in xprincipal.T]))
print()
print("Columns are random points on the ellipsoid:")
print(xrandom)
print("Check:", np.array([x.dot(Hinv.dot(x)) for x in xrandom.T]))
Here's the output when the script is run. H is random, so the output will be different each time the script is run. The line beginning with Check: after each matrix shows the result of computing x.dot(Hinv.dot(x)) for each column. The values shown after Check: should all be y (with a small tolerance to allow for normal numerical imprecision).
Columns are the ellipsoid coordinate axis intercepts:
[[ 2.9341 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 2.752 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 2.0081 0. 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 4.3061 0. 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 3.4531 0. 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 1.7946 0. 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 3.5877 0. 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 1.8925 0. 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 1.2435 0. ]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 2.9075]]
Check: [ 3. 3. 3. 3. 3. 3. 3. 3. 3. 3.]
Columns are points where the ellipsoid is tangent to its bounding box:
[[ 4.2205 -1.6619 0.9486 -1.0971 0.0672 0.0988 2.0569 -0.2758 0.4345 -1.1246]
[-2.392 6.0745 -0.1126 0.262 0.1952 0.7275 -1.829 -3.3036 0.3353 -0.4161]
[ 1.2413 -0.1023 5.5224 -1.9892 1.3277 0.6662 0.6003 -2.6505 -1.0728 0.65 ]
[-1.3493 0.2239 -1.8697 5.1908 0.0367 -0.9623 0.1469 1.5594 -0.3419 0.4431]
[ 0.0917 0.1851 1.385 0.0407 5.7611 -2.3986 0.884 0.1803 -2.3425 -1.4966]
[ 0.1385 0.7082 0.7134 -1.0963 -2.4621 5.9136 -2.6088 -0.8365 4.7242 -0.2406]
[ 2.5176 -1.5554 0.5615 0.1462 0.7926 -2.2789 5.1657 0.0131 -1.8862 -0.0804]
[-0.3829 -3.1874 -2.8128 1.7606 0.1834 -0.829 0.0149 5.8607 -1.2844 2.1692]
[ 0.4579 0.2456 -0.8642 -0.293 -1.8089 3.5539 -1.6244 -0.9749 4.4486 -1.8706]
[-1.4002 -0.3599 0.6185 0.4485 -1.3651 -0.2138 -0.0818 1.945 -2.2096 5.2549]]
Check: [ 3. 3. 3. 3. 3. 3. 3. 3. 3. 3.]
Columns are points where the principal axes of the ellipsoid intersect the ellipsoid:
[[-0.4701 1.1006 -3.008 1.1252 -0.8771 0.3136 -1.0045 2.0293 0.2615 -0.0509]
[ 3.2968 1.5837 4.3875 -0.4139 -0.9073 -0.2182 -1.6669 0.5303 -0.3532 0.2126]
[ 0.9165 3.6613 -1.9066 -2.764 1.0091 1.727 0.7535 0.1335 -0.5318 0.3281]
[-1.5272 -1.9226 2.4674 1.0623 -0.8445 3.5199 0.6734 0.3716 0.018 -0.0609]
[-2.2736 3.3975 1.2729 1.3181 3.3424 0.6659 -1.0468 -0.2749 0.5697 -0.0946]
[ 4.6168 -2.0728 -1.9233 -0.4141 1.2233 1.3196 -1.3411 -0.447 -0.3202 -0.3887]
[-2.7789 1.8796 -1.6604 0.6303 -2.7613 0.7791 -1.534 -1.2874 -0.1734 0.0563]
[-3.7189 -3.8936 -0.3987 -0.0928 1.7785 -0.2127 -1.1247 0.2619 -0.7321 0.3339]
[ 3.2782 -1.6147 -1.2554 1.8212 0.203 0.5629 -0.1255 -0.4354 0.8151 0.5622]
[-1.3981 -1.6701 0.4087 -4.573 -0.423 0.279 -0.8141 0.0621 0.9307 -0.0114]]
Check: [ 3. 3. 3. 3. 3. 3. 3. 3. 3. 3.]
Columns are random points on the ellipsoid:
[[ 1.5979 -1.8849 0.4878 -1.8069 -0.8968]
[-0.6583 -0.304 0.5729 -0.6411 1.1796]
[-0.857 -1.0776 1.4855 -2.2664 -1.6846]
[ 0.1828 0.3555 2.4142 2.7053 3.0825]
[-0.4522 0.6217 3.8429 -2.4424 0.0587]
[-0.6646 -2.4867 -0.3544 2.0967 -2.9529]
[-1.0759 -1.2378 0.7088 -0.561 0.2613]
[ 2.6662 2.862 0.3385 0.9958 0.821 ]
[-1.0947 -3.0513 -0.9832 2.4314 -1.6179]
[ 0.9955 2.3737 0.14 -0.1343 -1.0845]]
Check: [ 3. 3. 3. 3. 3.]