Multi-layer neural network won't predict negative values

Question

I have implemented a multilayer perceptron to predict the sin of input vectors. The vectors consist of four -1,0,1's chosen at random and a bias set to 1. The network should predict the sin of sum of the vectors contents.

eg Input = <0,1,-1,0,1> Output = Sin(0+1+(-1)+0+1)

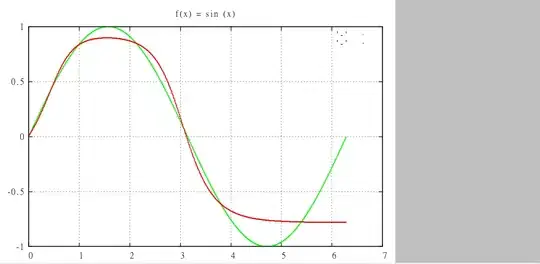
The problem I am having is that the network will never predict a negative value and many of the vectors' sin values are negative. It predicts all positive or zero outputs perfectly. I am presuming that there is a problem with updating the weights, which are updated after every epoch. Has anyone encountered this problem with NN's before? Any help at all would be great!!

note: The network has 5inputs,6hidden units in 1 hidden layer and 1 output.I am using a sigmoid function on the activations hidden and output layers, and have tried tonnes of learning rates (currently 0.1);

score 13 · Accepted Answer · edited Feb 24 '11 at 15:51

13

Being a long time since I looked into multilayer perceptrons hence take this with a grain of salt.

I'd rescale your problem domain to the [0,1] domain instead of [-1,1]. If you take a look at the logistic function graph:

enter image description here

It generates values between [0,1]. I do not expect it to produce negative results. I might be wrong, tough.

EDIT:

You can actually extend the logistic function to your problem domain. Use the generalized logistic curve setting A and K parameters to the boundaries of your domain.

Another option is the hyperbolic tangent, which goes from [-1,+1] and has no constants to set up.

edited Feb 24 '11 at 15:51

Phil

6,561
4
44
69

answered Feb 24 '11 at 14:30

Vitor Py

5,145
4
39
62

Thanks a lot, that does make sense! Il have to have a look around for a function that can allow for negative values. Unfortunately I cant change the problem domain as its an assignment for college. Thanks again! – B. Bowles Feb 24 '11 at 14:37
@B. Bowles Updated my answer with a possible solution. – Vitor Py Feb 24 '11 at 14:41
Thats great I'l give that a try now! There are a lot of params in that formula that don't apply to this network, and maths is definatly not my strongpoint. It certainly sounds like the way forward though. – B. Bowles Feb 24 '11 at 14:53
1

@B. Bowles The hyperbolic tangent also goes from [-1,+1] and has no constants to set up. I just remembered it now. – Vitor Py Feb 24 '11 at 15:00
Thats great, and far easier to implement!! my $a = exp($activation); my $b = exp(-$activation); $output = ($a-$b)/($a+$b); ...Just incase anyones interested in using it in future. Thanks a million – B. Bowles Feb 24 '11 at 15:50

score 4 · Answer 2 · answered Feb 24 '11 at 14:40

4

There are many different kinds of activation functions, many of which are designed to output a value from 0 to 1. If you're using a function that only outputs between 0 and 1, try adjusting it so that it outputs between 1 and -1. If you were using FANN I would tell you to use the FANN_SIGMOID_SYMMETRIC activation function.

answered Feb 24 '11 at 14:40

Phil

6,561
4
44
69

unfortunatly I can't make use of any libs for this assignment, if only! I have a look into how that works though, thanks a lot – B. Bowles Feb 24 '11 at 14:54

score 0 · Answer 3 · answered Nov 24 '19 at 18:10

Although the question has already been answered, allow me to share my experience. I have been trying to approximate Sine function using a 1--4--1 neural network. i.e, And similar to your case, I am not allowed to use any high level API like TensorFlow. Moreover I am bound to use C++ over Python3! (BTW, I mostly prefer C++).

I used Sigmoid activation and its derivative defined as:

double sigmoid(double x) 
{ 
   return 1.0f / (1.0f + exp(-x)); 
}

double Sigmoid_derivative(double x)
{
   return x * (1.0f - x);
}

And this is what I got after 10,000 epochs, training the network on 20 Training Examples.

As, you can see, the network didn't feel like the negative curve. So, I changed the activation function to Tanh.

double tanh(double x)
{
   return (exp(x)-exp(-x))/(exp(x)+exp(-x));
}

double tanh_derivative(double x)
{
   return 1.0f - x*x ;
}

And surprisingly, after half the epochs, (i.e., 5000), I got a far better curve. And we all know that it will significantly improve on using more hidden neurons, more epochs and better (and more) training example. Also, shuffling the data is important too!

Multi-layer neural network won't predict negative values

3 Answers3

Linked