3D Z-Y-X rotation of vector

Question

I'm trying to rotate a vector in 3 dimensions by creating a rotation matrix from the world to the new rotation. I do the rotation by first rotating around the Z axis, then the Y axis and lastly the X axis using right hand notation.

The matrix I use can be found on wikipedia (http://en.wikipedia.org/wiki/Euler_angles). It's located slightly below the middle of the page in the list of transformation matrices. I'm using the ZYX one:

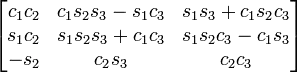
I now create it with a Z rotation of +45 degrees, a Y rotation of +45 degrees and no X rotation. This gives me the following matrix:

[  0.5   -0.707 0.5   ]
[  0.5    0.707 0.5   ]
[ -0.707  0.0   0.707 ]

Now I multiply it by the following vector:

[ 10 ]
[  0 ]
[  0 ]

As can be seen it's a 10 unit long vector along the x-axis. I expect the rotated result to be around 6 in the x, y, and z field (with z being negative) as that gives a vector of roughly length 10. Ie the vector is rotated first exactly between the world x and y axis (the first z rotation) and then angled down from there another 45 degrees ending up exactly between the x-y plane and the negative z axis (the second y rotation). In my mind this means three equally long unit vectors representing this vector.

However, both my matrix class and all other programs give me this vector as result:

[  5    ]
[  5    ]
[ -7.07 ]

It seems correct as the length of it is 10 as expected. So the question is where am I wrong? I'm sure I'm making some stupid thought error somewhere obvious, because it sure doesn't have three equally long arms :p

Answer 1

The ZYX Euler angle rotation matrix is defined as

R_ZYX(dz, dy, dx) = R(Z, dz) * R(Y, dy) * R(X, dx)

There are two different ways of reading the order of the rotations: either from left to right or from right to left. When read from left to right the rotations are about the local axes of the coordinate frame, as you are correctly doing. It's only when read from right to left that the rotations are about a fixed coordinate frame.

Now to answer the question, let's compute the angle dy you should be rotating with if you want all coordinates of the rotated vector to have the same absolute value.

Let r be the length of v and let a be the absolute coordinate value. By Pythogoras, a^2 + a^2 + a^2 = r^2, hence a = r / sqrt(3). The angle of the rotated vector relative to the XY plane is dy = asin(a / r) = asin(1 / sqrt(3)), which is about 35.3 degrees. This angle is different from the 45 degrees (or asin(1 / sqrt(2)) in radians) that you are currently using.

A test (using Python and the gameobjects library):

from gameobjects import *
from math import *
import random

V = vector3.Vector3
T = matrix44.Matrix44

def R_x(dx): return T.x_rotation(dx)
def R_y(dy): return T.y_rotation(dy)
def R_z(dz): return T.z_rotation(dz)

def fmt(v): return "(%.3f, %.3f, %.3f)" % (v[0], v[1], v[2])

dx = 0
dy = asin(1 / sqrt(3.0))
dz = pi / 4

v = V(10, 0, 0)

print "ZYX Euler angle transformations:"
print fmt((R_z(dz) * R_y(dy) * R_x(dx)).transform(v))
dy = pi / 4
print fmt((R_z(dz) * R_y(dy) * R_x(dx)).transform(v))

The output:

ZYX Euler angle transformations:
(5.774, 5.774, -5.774)
(5.000, 5.000, -7.071)

The last line for dz = dy = pi / 4 shows that the program agrees with your Euler angle implementation.

Answer 2

Remember that the second rotation is relative to the axis, not the vector. After rotating in the XY plane, imagine that whole plane twisting 45 degrees around the Y axis. This is not the same as twisting your rotated vector straight up (i.e. rotating around X=-Y) until it's at 45 degrees to the XY plane. Hard to explain, but I hope that helps :-)

(Edit: got the axes the right way round)