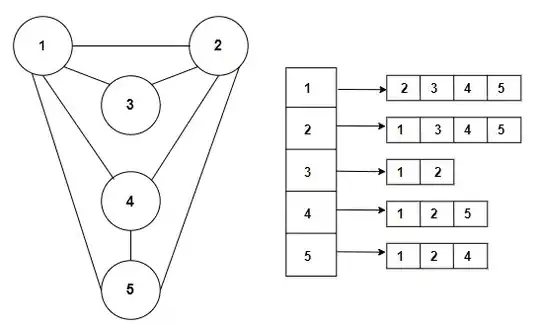
I recently had to take a look at the Dijkstra algorithm and it's proof.
The proof of the algorithm terminates in all sources I could find with the equality of quantity of all vertices and the quantity of all vertices visited (e.g. R=V or S=V). Moreover the while-loop of this algorithm terminates when Q (initiated as all vertices of the graph) is empty, so all vertices have to be visited.
I don't get why this has to be the case. Aren't there graphs where the algorithm doesn't has to visit all vertices e.g.: The start vertex is connected to the "find" vertex directly with weight 1 and to other vertices with weight 10.
I hope you get the problem I have here.
Edit: This is the pseudo-code I used from Cormen: