Lets break it step wise to understand the code better.
The below block of code creates a tensor x of shape (1,3)
x = torch.ones(3, requires_grad=True)
print(x)
>>> tensor([1., 1., 1.], requires_grad=True)
The below block of code creates a tensor y by multiplying each element of x by 2
y = x * 2
print(y)
print(y.requires_grad)
>>> tensor([2., 2., 2.], grad_fn=<MulBackward0>)
>>> True
TORCH.data returns a tensor whose requires_grad is set to false
print(y.data)
print('Type of y: ', type(y.data))
print('requires_grad: ', y.data.requires_grad)
>>> tensor([2., 2., 2.])
>>> Type of y: <class 'torch.Tensor'>
>>> requires_grad: False
TORCH.norm() Returns the matrix norm or vector norm of a given tensor. By default it returns a Frobenius norm aka L2-Norm which is calculated using the formula
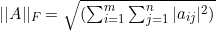 .
.
In our example since every element in y is 2, y.data.norm() returns 3.4641 since  is equal to 3.4641
is equal to 3.4641
print(y.data.norm())
>>> tensor(3.4641)
The below loop is run until the norm value is less than 1000
while y.data.norm() < 1000:
print('Norm value: ', y.data.norm(), 'y value: ', y.data )
y = y * 2
>>> Norm value: tensor(6.9282) y value: tensor([4., 4., 4.])
>>> Norm value: tensor(3.4641) y value: tensor([2., 2., 2.])
>>> Norm value: tensor(13.8564) y value: tensor([8., 8., 8.])
>>> Norm value: tensor(27.7128) y value: tensor([16., 16., 16.])
>>> Norm value: tensor(55.4256) y value: tensor([32., 32., 32.])
>>> Norm value: tensor(110.8512) y value: tensor([64., 64., 64.])
>>> Norm value: tensor(221.7025) y value: tensor([128., 128., 128.])
>>> Norm value: tensor(443.4050) y value: tensor([256., 256., 256.])
>>> Norm value: tensor(886.8100) y value: tensor([512., 512., 512.])
>>>
>>> Final y value: tensor([1024., 1024., 1024.], grad_fn=<MulBackward0>)
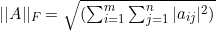 .
.
 is equal to 3.4641
is equal to 3.4641