curve fitting equations python

Question

I am trying to fit data with an admittance equation for an rlc circuit having 6 components. I am following an example given he[fit]1re and inserted my equation. The equation is the real part of admittance for the 6 component circuit simplified using Mathcad. In the figure attached the x axis is omega (w=2*pi*f) and y is admittance in milli Siemens.

The program runs but it doesn't do the fitting despite a good trial function. I appreciate any help why the fit is a straight line. I attached also a Gaussian fitting example.

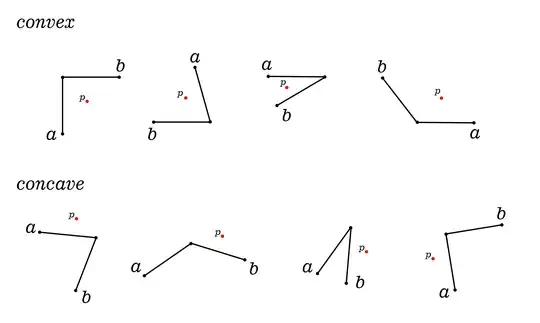
this is what i get when I try to fit with the equation. The data is the one with a smaller peak on the left and the trial function is the dotted line. the fit is a straight line

from numpy import sqrt, pi, exp, linspace, loadtxt
from lmfit import  Model

import matplotlib.pyplot as plt

data = loadtxt("C:/Users/susu/circuit_eq_real5.dat")
x = data[:, 0]
y = data[:, 1]

def circuit(x,C0,Cm,Lm,Rm,R0,Rs):


    return ((C0**2*Cm**2*Lm**2*R0*x**4)+(Rs*C0**2*Cm**2*Lm**2*x**4)+(C0**2*Cm**2*R0**2*Rm*x**2)+(Rs*C0**2*Cm**2*R0**2*x**2)+(C0**2*Cm**2*R0*Rm**2*x**2)+(2*Rs*C0**2*Cm**2*R0*Rm*x**2)+(Rs*C0**2*Cm**2*Rm**2*x**2)-(2*C0**2*Cm*Lm*R0*x**2)-(2*Rs*C0**2*Cm*Lm*x**2)+(C0**2*R0)+(Rs*C0**2)-(2*Rs*C0*Cm**2*Lm*x**2)+(2*Rs*C0*Cm)+(Cm**2*Rm)+(Rs*Cm**2))/((C0**2*Cm**2*Lm**2*x**4)+(C0**2*Cm**2*R0**2*x**2)+(2*C0**2*Cm**2*R0*Rm*x**2)+(C0**2*Cm**2*Rm**2*x**2)-(2*C0**2*Cm*Lm*x**2)+(C0**2)-(2*C0*Cm**2*Lm*x**2)+(2*C0*Cm)+(Cm**2))

gmodel = Model(circuit)
result = gmodel.fit(y, x=x, C0=1.0408*10**(-12), Cm=5.953*10**(-14), 
Lm=1.475*10**(-7), Rm=1.571, R0=2.44088, Rs=0.42)

print(result.fit_report())

plt.plot(x, y,         'bo')
plt.plot(x, result.init_fit, 'k--')
plt.plot(x, result.best_fit, 'r-')
plt.show()

Below is the Fit Report

 [[Fit Statistics]]
# fitting method   = leastsq
# function evals   = 14005
# data points      = 237
# variables        = 6
chi-square         = 32134074.5
reduced chi-square = 139108.548
Akaike info crit   = 2812.71607
Bayesian info crit = 2833.52443
[[Variables]]
C0: -7.5344e-15 +/- 6.3081e-09 (83723736.65%) (init = 1.0408e-12)
Cm: -8.9529e-13 +/- 1.4518e-06 (162164237.47%) (init = 5.953e-14)
Lm:  2.4263e-06 +/- 1.94051104 (79978205.20%) (init = 1.475e-07)
Rm: -557.974399 +/- 1.3689e+09 (245334051.75%) (init = 1.571)
R0: -5178.53517 +/- 6.7885e+08 (13108904.45%) (init = 2.44088)
Rs:  2697.67659 +/- 7.3197e+08 (27133477.70%) (init = 0.42)
[[Correlations]] (unreported correlations are < 0.100)
C(R0, Rs) = -1.003
C(Rm, Rs) = -0.987
C(Rm, R0) =  0.973
C(C0, Lm) =  0.952
C(C0, Cm) = -0.502
C(Cm, R0) = -0.483
C(Cm, Rs) =  0.453
C(Cm, Rm) = -0.388
C(Cm, Lm) = -0.349
C(C0, R0) =  0.310
C(C0, Rs) = -0.248
C(C0, Rm) =  0.148

Thank you so much M Newville and Mikuszefski and others for your insights and feedback. I agreed what I put there is perhaps a mess to put in a program. It is apparent from the python code that I am not versed in Python or programming.

Mikuszefsky, thanks for posting the rlc example code. Your approach is neat and interesting. I didn't know Python does direct complex fitting.I will try your approach and see if can do the fit. I want to fit both the real and imaginary part of Y (admittance). I will definitely get stuck somewhere and will post my progress here. Best, Susu

Answer 1

Here a way to clean up RLC circuits with parallel and series connections. This avoids this super long line and hard to check function. It also avoids Matlab or similar programs, as it directly computes the circuit. Surely, it can be extended easily the OP's circuit. As pointed out by M Newville, the simple fit fails. If, on the other hand, units are scaled to natural units, it works even without initial parameters. Note, results are onnly correct by a scaling factor. One needs to know at least one components value.

import matplotlib.pyplot as plt
import numpy as np
from scipy.optimize import curve_fit

def r_l( w, l ):
    return 1j * w * l

def r_c( w, c ):
    return 1. / ( 1j * w * c )

def parallel( a, b ):
    return( 1. / ( 1./ a + 1. / b ) )

def series( a, b ):
    return a + b

# simple rlc band pass filter (to be extended)
def rlc_band( w , r, l, c ):
    lc = parallel( r_c( w , c ), r_l( w, l ) )
    return lc / series( r, lc )

def rlc_band_real( w , r, l, c ):
    return rlc_band( w , r, l, c ).real

def rlc_band_real_milli_nano( w , r, l, c ):
    return rlc_band_real( w , r, 1e-6 * l, 1e-9 * c ).real

wList = np.logspace( 5, 7, 25 )
wFullList = np.logspace( 5, 7, 500 )
rComplexList = np.fromiter( ( rlc_band(w, 12, 1.3e-5, 1e-7 ) for w in wList ), np.complex )
rList = np.fromiter( ( r.real for r in rComplexList ), np.float )
pList = np.fromiter( ( np.angle( r ) for r in rComplexList ), np.float )

fit1, pcov = curve_fit( rlc_band_real, wList, rList )
print fit1
print "does not work"

fit2, pcov = curve_fit( rlc_band_real_milli_nano, wList, rList )
print fit2
print "works, but is not unique (scaling is possible)"
print 12, fit2[1] * 12 / fit2[0], fit2[2] * fit2[0] / 12.

fig = plt.figure()
ax = fig.add_subplot( 1, 1, 1 )

ax.plot( wList, rList , ls='', marker='o', label='data')
#~ ax.plot( wList, pList )
ax.plot( wFullList, [ rlc_band_real( w , *fit1 ) for w in wFullList ], label='naive fit')
ax.plot( wFullList, [ rlc_band_real_milli_nano( w , *fit2 ) for w in wFullList ], label='scaled units')
ax.set_xscale('log')
ax.legend( loc=0 )

plt.show()

Providing:

>> /...minpack.py:785: OptimizeWarning: Covariance of the parameters could not be estimated category=OptimizeWarning)
>> [1. 1. 1.]
>> does not work
>> [ 98.869924   107.10908434  12.13715912]
>> works, but is not unique (scaling is possible)
>> 12 13.0 100.0

Answer 2

Providing a real link to a text file of the actual data you are using and/or a real plot of what you are actually seeing would be most helpful. Also, please provide an accurate and complete description of the results including the text of what is actually printed out by the print(result.fit_report()). Basically, ask yourself how you might try to help someone who asked such a question, and provide as much information as you can.

No one (including you) is ever going to be able to spell-check the implementation of your function. You will need thorough and robust testing of this function in order to convince anyone (including you, I hope) that it is doing what you think it should do. You should provide the results of those tests before worrying about why it is not working as a fitting function. You should definitely consider refactoring that mess of an equation into more manageable and readable pieces.

That said, I also strongly recommend that you do not work in units of Farads and Henrys but picoFarads or nanoFarads and microHenrys. That will make the values much closer to 1 (say, order 1e-6 to 1e+6), which will make it much easier for the fit to do its job.