Project vector w onto vector v and draw perpendicular line - preparation for PCA

Question

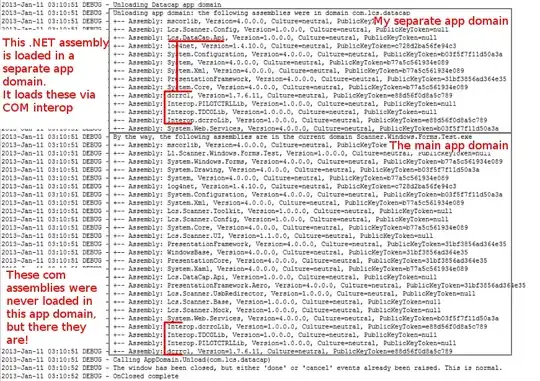
I want to do vector projection as preparation for PCA where I followed This tutorial for the calculation of the vector projection. 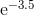w is the vector which 'points' onto the data points, v is the vector which spans the line onto which w should be projected.

The code is:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
style.use('fivethirtyeight')
from sklearn.preprocessing import StandardScaler

# Normalize the input data
A = np.array([[10,8],[1,2],[7,5],[3,5],[7,6],[8,7],[9,9],[4,5],[6,5],[6,8],
             [1,9],[10,2],[6,3],[2,5],[1,14],[8,8],[9,5],[4,4],[5,6],[8,8],
             [11,9],[10,12],[6,4],[5,2],[10,2],[8,3],[6,9],[0,4],[13,6],[9,6]])

A = StandardScaler(with_std=False,copy=False).fit_transform(A)


fig = plt.figure(figsize=(15,10))
ax0 = fig.add_subplot(111)
ax0.set_ylim(bottom=min(A[:,1])-3,top=max(A[:,1])+3)

ax0.scatter(A[:,0],A[:,1])

# Initialize a first vector a

v = np.array([1,0.5])




# Plot the vector v
#ax0.arrow(0,0,a[0],a[1],length_includes_head=True,width=0.03,color='green')


# Plot the line y=alpha*v defined by the vector a and passing the origin
ax0.plot(np.linspace(min(A[:,0])-3,max(A[:,0])+3),np.linspace(min(A[:,0])-3,max(A[:,0])+3)*(v[1]/v[0]),
         'k--',linewidth=1.5,zorder=0)

# Run through all datapoints

coordinates_on_ba_run = [] # Store the coordinates of the projected points on a 

for i in range(len(A[:,0])):
    # Plot the vector v
    #ax0.arrow(0,0,v[0],v[1],length_includes_head=True,width=0.03,color='green')


    # Point on one of the datapoints and denote this vector with w
    w = np.array([A[i][0],A[i][1]])
    #ax0.arrow(0,0,w[0],w[1],length_includes_head=True,width=0.03,color='blue')

    # Caclculate c and the projection vector cv. Additionally, test if the dot product of v and (w-cv) is zero

    c = np.dot(w,v.reshape(2,1))/np.dot(v,v.reshape(2,1))
    print(np.dot((w-c*v),v)) #This must be zero for each projection!
    cv = c*v

 

    # Draw a line from the datappoint in A to the tip of the vector cv. 


    ax0.plot([w[0],cv[0]],[w[1],cv[1]],linewidth=1,color='red',linestyle='--',zorder=0)



    
plt.show()

This gives the following result:

2.22044604925e-16
-2.22044604925e-16
0.0
0.0
2.77555756156e-17
-5.55111512313e-17
1.11022302463e-16
2.22044604925e-16
0.0
0.0
0.0
0.0
0.0
-2.22044604925e-16
0.0
-2.22044604925e-16
0.0
1.11022302463e-16
0.0
-2.22044604925e-16
0.0
-4.4408920985e-16
0.0
0.0
0.0
0.0
0.0
-2.22044604925e-16
-4.4408920985e-16
-2.22044604925e-16

So the code is working and also the 'control' calculations (np.dot((w-c*v),v))which must be zero for each transformation are zero... Hence the results should be correct... BUT, as you can see by the naked eye, the dashed lines are not perpendicular to the line spanned by the vector v. So is this only a visualization issue or is there an error in the code? Appreciate any help

score 0 · Accepted Answer · answered May 24 '18 at 18:15

Have found the error... If you look at the ratio of the axes, you see that they are not equal, that is, the x axis has limits (-10,10) while the y axis has limits (-6,10)... Consequently this distorts the view and by the naked eye the angles between the red dashed line and the line spanned by v is not 90 degree but something else depending on the ratio. This also explains why the calculation np.dot((w-c*v),v) returns zero which indicates that the results are correct.

Here is the working code:

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import style
style.use('fivethirtyeight')
from sklearn.preprocessing import StandardScaler


# Normalize the input data
A = np.array([[10,8],[1,2],[7,5],[3,5],[7,6],[8,7],[9,9],[4,5],[6,5],[6,8],
             [1,9],[10,2],[6,3],[2,5],[1,14],[8,8],[9,5],[4,4],[5,6],[8,8],
             [11,9],[10,12],[6,4],[5,2],[10,2],[8,3],[6,9],[0,4],[13,6],[9,6]])

A = StandardScaler(with_std=False,copy=False).fit_transform(A)

fig = plt.figure(figsize=(10,10))
ax0 = fig.add_subplot(111)
ax0.set_aspect('equal')
ax0.set_xlim((-10,10))
ax0.set_ylim((-10,10))

ax0.scatter(A[:,0],A[:,1])


# Run through all the data

for i in range(len(A[:,0])):

    # v
    v = np.array([3,2])
    ax0.plot(np.linspace(-10,10),np.linspace(-10,10)*(v[1]/v[0]),color='black',linestyle='--',linewidth=1.5)   

    # w
    w = np.array([A[i][0],A[i][1]])
    #ax0.arrow(0,0,w[0],w[1],length_includes_head=True,width=0.01,color='green')

    # cv
    cv = (np.dot(w,v))/np.dot(v,np.transpose(v))*v
    #ax0.arrow(0,0,cv[0],cv[1],length_includes_head=True,width=0.005,color='black')
    print(cv)

    # line between w and cv
    ax0.plot([w[0],cv[0]],[w[1],cv[1]],'r--',linewidth=1.5)


    # Check the result
    print(np.dot((w-cv),cv))

plt.show()

Project vector w onto vector v and draw perpendicular line - preparation for PCA

1 Answers1