I am trying to implement a simple EM algorithm. So far, it seems to be working well except for the small problem that variances quickly shrink to zero, converging around the mean of the data. (If I do not update the variances, it will converge to the mean completely fine!)
As far as I can tell, this is due to "weighting" the points close to the centre too heavily - hence making the algorithm lower the variance and shrink to zero. When I change the formula from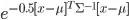 
to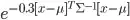 
the algorithm works much better (apart from slightly overestimating variance, which is to be expected). Is this a problem with my code?
class DataPoint {
int nDims; // Number of dimensions
float[] data;
DataPoint(int n) {nDims = n; data = new float[n];}
DataPoint(float[] d) {nDims = d.length; data = d;}
}
float sum(float[] d) {float ret = 0; for (int i = 0; i < d.length; ++i) {ret += d[i];} return ret;}
float[] sub(float[] f, float[] u) {float[] ret = new float[f.length]; for (int i = 0; i < f.length; ++i) {ret[i] = f[i] - u[i];} return ret;}
float distSq(float[] d) {float ret = 0; for (int i = 0; i < d.length; ++i) {ret += d[i]*d[i];} return ret;}
float distSq(float[][] d) {float ret = 0; for (int i = 0; i < d.length; ++i) {ret += distSq(d[i]);} return ret;}
float det(float[][] mat) {
if (mat.length == 2 && mat[0].length == 2) {
float det = (mat[0][0] * mat[1][1]) - (mat[0][1] * mat[1][0]);
return det;
}
throw new RuntimeException("Det has to be 2x2");
}
float[][] inverse(float[][] mat) {
if (mat.length == 2 && mat[0].length == 2) {
float det = mat[0][0] * mat[1][1] - mat[0][1] * mat[1][0];
float[][] ret = {{mat[1][1]/det, -mat[0][1]/det}, {-mat[1][0]/det, mat[0][0]/det}};
return ret;
}
throw new RuntimeException("Inverse has to be 2x2");
}
class GMM {
int number;
int dims;
float[] weights;
float[][] means;
float[][][] covariances;
float[][][] invCov;
GMM(int gNo, int noDimensions) {
number = gNo;
dims = noDimensions;
weights = new float[gNo];
means = new float[gNo][noDimensions];
covariances = new float[gNo][noDimensions][noDimensions];
invCov = new float[gNo][noDimensions][noDimensions];
// Initialise to random values.
for (int i = 0; i < gNo; ++i) {
weights[i] = random(0, 1);
for (int j = 0; j < noDimensions; ++j) {
means[i][j] = random(-100,100);
covariances[i][j][j] = 100;
invCov[i] = inverse(covariances[i]);
}
}
normaliseWeights();
}
float[][] EStep(DataPoint[] data) {
// For each data point, return probablility of each gaussian having generated it
// Arguments: n-dimensional data
float[][] ret = new float[number][data.length];
for (int Gauss = 0; Gauss < number; ++Gauss) {
for (int i = 0; i < data.length; ++i) {
ret[Gauss][i] = calculateProbabilityFast(data[i], Gauss);
}
}
return ret;
}
void MStep(DataPoint[] data, float[][] dataProbabilities) {
for (int Gauss = 0; Gauss < number; ++Gauss) {
means[Gauss] = new float[data[0].nDims]; // Reset dims to zero
float probSum = 0;
for (int i = 0; i < dataProbabilities[Gauss].length; ++i) {
probSum += dataProbabilities[Gauss][i];
for (int j = 0; j < means[Gauss].length; ++j) {
means[Gauss][j] += data[i].data[j] * dataProbabilities[Gauss][i];
}
}
for (int i = 0; i < means[Gauss].length; ++i) {
means[Gauss][i] /= probSum; // Normalise
}
// Means[Gauss] has been updated
// Now for covariance.... :x
covariances[Gauss] = new float[data[0].nDims][data[0].nDims];
for (int m = 0; m < data[0].nDims; ++m) {
for (int n = 0; n < data[0].nDims; ++n) {
for (int i = 0; i < dataProbabilities[Gauss].length; ++i) {
covariances[Gauss][m][n] += (data[i].data[m]-means[Gauss][m])*(data[i].data[n]-means[Gauss][n])*dataProbabilities[Gauss][i];
}
}
}
// Created a triangular matrix, normalise and then update other half too.
for (int m = 0; m < data[0].nDims; ++m) {
for (int n = 0; n < data[0].nDims; ++n) {
covariances[Gauss][m][n] /= probSum;
}
}
// Update inverses
invCov[Gauss] = inverse(covariances[Gauss]);
weights[Gauss] = probSum;
}
normaliseWeights();
}
float calculateProbabilityFast(DataPoint x, int Gauss) {
float ret = pow(TWO_PI, dims/2.0)*sqrt(det(covariances[Gauss]));
float exponent = 0;
for (int i = 0; i < x.nDims; ++i) {
float temp = 0;
for (int j = 0; j < x.nDims; ++j) {
temp += (x.data[j] - means[Gauss][j])*invCov[Gauss][i][j];
}
exponent += temp*(x.data[i] - means[Gauss][i]);
}
exponent = exp(-0.5*exponent);
// ==================================================================
// If I change this line HERE to -0.3*exponent, everything works fine
// ==================================================================
//print(exponent); print(","); println(ret);
return exponent/ret;
}
void normaliseWeights() {
float sum = sum(weights);
for (int i = 0; i < number; ++i) {weights[i] /= sum;}
}
void display() {
ellipseMode(CENTER);
for (int i = 0; i < number; ++i) {
//strokeWeight(weights[i]*100);
strokeWeight(5);
stroke(color(255, 0, 0));
point(means[i][0], means[i][1]);
noFill();
strokeWeight(1.5);
ellipse(means[i][0], means[i][1], (covariances[i][0][0]), (covariances[i][1][1]));
ellipse(means[i][0], means[i][1], (covariances[i][0][0]*2), (covariances[i][1][1]*2));
fill(0);
}
}
}
DataPoint[] data;
final int size = 10000;
GMM MixModel;
void setup() {
// Hidden gaussians
size(800,600);
MixModel = new GMM(1, 2); // 1 gaussians, 2 dimensions.
data = new DataPoint[size];
int gNo = 1;
float gxMeans[] = new float[gNo];
float gxVars[] = new float[gNo];
float gyMeans[] = new float[gNo];
float gyVars[] = new float[gNo];
float covars[] = new float[gNo];
for (int i = 0; i < gNo; ++i) {
gxMeans[i] = random(-100, 100);
gxVars[i] = random(5, 40);
gyMeans[i] = random(-100, 100);
gyVars[i] = random(5, 40); // Actually std. devs!!
covars[i] = 0;//random(-1, 1);
println("Vars: " + str(pow(gxVars[i], 2)) + ", " + str(pow(gyVars[i], 2)));
println("Covar: " + str(covars[i]));
}
for (int i = 0; i < size; ++i) {
int gauss = (int)random(gNo);
data[i] = new DataPoint(2);
data[i].data[0] = randomGaussian()*gxVars[gauss] + gxMeans[gauss];
data[i].data[1] = (randomGaussian()*gyVars[gauss])*(1-abs(covars[gauss]))+(gyVars[gauss]*covars[gauss]*(data[i].data[0]-gxMeans[gauss])/gxVars[gauss]) + gyMeans[gauss];
}
frameRate(5); // Let's see what's happening!
}
void draw() {
translate(width/2, height/2); // set 0,0 at centre
background(color(255, 255, 255));
stroke(0);
strokeWeight(1);
for (int i = 0; i < size; ++i) {
point(data[i].data[0], data[i].data[1]);
}
MixModel.display();
float[][] dataProbs = MixModel.EStep(data);
MixModel.MStep(data, dataProbs);
print(MixModel.covariances[0][0][0]); print(", ");
println(MixModel.covariances[0][1][1]);
}
EDIT: Complete, minimal working example. The variance still converges to 0, so this suggests perhaps I'm doing something wrong with the algorithm?
import random, statistics, math
hiddenMu = random.uniform(-100, 100)
hiddenVar = random.uniform(10, 30)
dataLen = 10000
data = [random.gauss(hiddenMu, hiddenVar) for i in range(dataLen)]
hiddenVar **= 2 # Make it the actual variance rather than std. dev.
print("Variance: " + str(hiddenVar) + ", actual: " + str(statistics.variance(data)))
print("Mean : " + str(hiddenMu ) + ", actual: " + str(statistics.mean (data)))
guessMu = random.uniform(-100, 100)
guessVar = 100
print("Initial mu guess: " + str(guessMu))
print("Initial var guess: " + str(guessVar))
# perform iterations
numIters = 100
for i in range(numIters):
dataProbs = [math.exp(-0.5*((i-guessMu)**2)/guessVar)/((2*math.pi*guessVar)**0.5) for i in data]
guessMu = sum(map(lambda x: x[0]*x[1], zip(dataProbs, data)))/sum(dataProbs)
guessVar = sum(map(lambda x: x[0]*((x[1]-guessMu)**2), zip(dataProbs, data)))/sum(dataProbs)
print(str(i) + " mu guess: " + str(guessMu))
print(str(i) + " var guess: " + str(guessVar))
print()
EDIT 2: Could I need something like Bessel's correction? (multiply the result by n/(n-1)). If so, how would I go about doing this when the sum of the probabilities themselves may be less than one?
