3

I am using the Gauss-Laguerre quadrature to approximate the following integral

First formula

I wrote the function in R

int.gl<-function(x)
{
 x^(-0.2)/(x+100)*exp(-100/x)
}

First, I used integrate() function to get the "true" value, which I double check with Wolfram Alpha

integrate(int.gl, lower = 0, upper = Inf)$value
[1] 1.627777

Then, I used glaguerre.quadrature() function

rule<-glaguerre.quadrature.rules(64, alpha = 0, normalized = F)[[64]]
glaguerre.quadrature(int.gl, lower = 0, upper = Inf, rule = rule, weighted = F)
[1] 0.03610346

Clearly, the result is far away from the true value. At that time, I thought I had to transform this function to include a e^(-x) term. So, let X = 1/Y. I obtained a different formula but the same integral

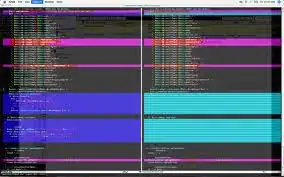
Second formula

In the same manner, I used the following R code 

int.gl2<-function(x)
{
 x^(-0.8)/(1+100*x)*exp(-100*x)
}
integrate(int.gl2, lower = 0, upper = Inf)$value
[1] 1.627777
glaguerre.quadrature(int.gl2, lower = 0, upper = Inf, rule = rule, weighted = F)
[1] 0.03937068

Well, two different values. Does the Gauss-Laguerre quadrature have trouble in finding this integral? Is there any other Gauss-type quadrature can help find this integral?

Note: I have to use Gauss-type quadrature since I am trying to find MLEs of some parameters for a customized distribution. For simplicity, I just fixed these parameters(these constants in the integral). However, integrate() function seems to be less "robust" than glaguerre.quadrature() function. (integrate() returns divergent error when optimizing the log-likelihood).

EDIT 1

According to Hans. W's comment, I check the use of glaguerre.quadrature with the following example. Suppose we wanna find the following integral

int.gl3<-function(x)
{
 ((x+100)/(x+200))^0.2*exp(-5*x)
}

glaguerre.quadrature(int.gl3, lower = 0, upper = Inf, rule = rule, weighted = F)
[1] 0.1741448
integrate(int.gl3, lower = 0, upper = Inf)$value
[1] 0.1741448

It seems like the use of glaguerre.quadrature is correct.

Let's check the transformation now. I transform this integral, by letting 100Y=X, such that it includes exp(-x).

int.gl4<-function(x)
{
 0.01^0.2*x^(-0.8)/(1+x)*exp(-x)
}
integrate(int.gl4, lower = 0, upper = Inf)$value
[1] 1.627777
glaguerre.quadrature(int.gl4, lower = 0, upper = Inf, rule = rule, weighted = F)
[1] 0.9621667

The result is more close to the true value but not exactly equal.

EDIT 2

Here is my complete example

Integration and false convergence of optimization in R

C.C.
  • 55
  • 9
  • I assume your use of `gaussquad::glaguerre.quadrature` is probably and the transformation of the integral is certainly incorrect; e.g. the exponential term must be `exp(-x)`. I tried `pracma::gaussLaguerre` with the corrected integrand and I failed, too. It seems like this function is converging to zero much too slowly for the in R available Gauss-Laguerre implementations. – Hans W. May 15 '18 at 18:10
  • @HansW. As you mentioned, it was improved but still not that good. – C.C. May 15 '18 at 21:58
  • Your transformed function `int.gl4` is now converging rapidly enough to be handled by `integrate`. Even integrating it over the interval `[0, 100]` is sufficient for double precision: `integrate(int.gl4, 0, 100)` will return "1.627777 with absolute error < 2.8e-05". – Hans W. May 16 '18 at 02:09
  • @HansW. For this example, yes, `integrate` can handle this integral perfectly. However, I intend to use Gauss-type quadrature which, I think, is more robust than `integrate` because `integrate` was more likely to returns divergent error when I did optimization to find MLEs. For simplicity, I fixed those parameters. That is the reason why you can see constants in the integral. – C.C. May 16 '18 at 02:35
  • 1
    As long as you do not provide a relevant example, it is difficult to help you. Basically, for integrating a badly converging function with Gauss-Laguerre, you will need many, many more nodes than those 64 you compute here. Saying that a procedure giving wrong results is better than one that is not robust -- that is a bit of a strange consideration in my eyes. – Hans W. May 16 '18 at 08:39
  • @HansW. Thank you for your response. I just edited my question and provided a complete example in another question. – C.C. May 22 '18 at 16:59

0 Answers0